题目内容
2.已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0<p1<p2<$\frac{1}{2}$,则( )| A. | E(ξ1)<E(ξ2),D(ξ1)<D(ξ2) | B. | E(ξ1)<E(ξ2),D(ξ1)>D(ξ2) | C. | E(ξ1)>E(ξ2),D(ξ1)<D(ξ2) | D. | E(ξ1)>E(ξ2),D(ξ1)>D(ξ2) |
分析 由已知得0<p1<p2<$\frac{1}{2}$,$\frac{1}{2}$<1-p2<1-p1<1,求出E(ξ1)=p1,E(ξ2)=p2,从而求出D(ξ1),D(ξ2),由此能求出结果.
解答 解:∵随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2,…,
0<p1<p2<$\frac{1}{2}$,
∴$\frac{1}{2}$<1-p2<1-p1<1,
E(ξ1)=1×p1+0×(1-p1)=p1,
E(ξ2)=1×p2+0×(1-p2)=p2,
D(ξ1)=(1-p1)2p1+(0-p1)2(1-p1)=${p}_{1}-{{p}_{1}}^{2}$,
D(ξ2)=(1-p2)2p2+(0-p2)2(1-p2)=${p}_{2}-{{p}_{2}}^{2}$,
D(ξ1)-D(ξ2)=p1-p12-(${p}_{2}-{{p}_{2}}^{2}$)=(p2-p1)(p1+p2-1)<0,
∴E(ξ1)<E(ξ2),D(ξ1)<D(ξ2).
故选:A.
点评 本题考查离散型随机变量的数学期望和方差等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
13.下列命题为真命题的是( )
| A. | 若p∧q为假命题,则p∨q为真命题 | |
| B. | 不存在实数α,β,使得等式tanα+tanβ=tan(α+β)成立 | |
| C. | 函数f(x)=ax2+bx+c为偶函数的充要条件是 b=0 | |
| D. | 若定义在R上的函数f(x)满足f(x)•f(x+1)=1,则f(x)是一个周期为1的函数 |
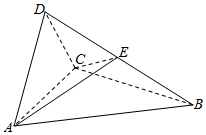 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.