题目内容

10．已知极坐标系的极点在直角坐标系的原点O，极轴与x轴非负半轴重合，曲线C1：ρsin2θ=4cosθ，C2：$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=tsinθ}\end{array}\right.$（t为参数），相交于A，B两点，若△AOB的面积为$\sqrt{6}$，则|AB|=6．

分析 求出曲线C1的直角坐标方程，把C2的参数方程代入C1得出弦长公式，根据三角形的面积公式列方程求出sinθ，从而可得|AB|的长．

解答 解：曲线C1的方程可化为ρ2sin2θ=4ρcosθ，即y2=4x，
把曲线C2的参数方程代入y2=4x得t2sin2θ=4+4tcosθ，即t2sin2θ-4tcosθ-4=0，
∴t1+t2=$\frac{4cosθ}{si{n}^{2}θ}$，t1t2=$\frac{-4}{si{n}^{2}θ}$，
∴|AB|=|t1-t2|=$\sqrt{（{t}_{1}+{t}_{2}）^{2}-4{t}_{1}{t}_{2}}$=$\frac{4}{si{n}^{2}θ}$，
∴S△AOB=$\frac{1}{2}×1×|AB|sinθ$=$\frac{2}{sinθ}$=$\sqrt{6}$，
∴sinθ=$\frac{\sqrt{6}}{3}$．
∴|AB|=$\frac{4}{si{n}^{2}θ}$=6．
故答案为：6．

点评 本题考查了极坐标与参数方程，参数的几何意义，属于中档题．

练习册系列答案
相关题目
20．曲线y=x2+$\frac{1}{x}$在点（1，2）处的切线方程为x-y+1=0．
1．如果一扇形的弧长变为原来的$\frac{3}{2}$倍，半径变为原来的一半，则该扇形的面积为原扇形面积的$\frac{3}{4}$．
18．已知复数z满足z（1+i）=2i，则z的共轭复数$\overline{z}$等于（　　）
A．1+iB．1-iC．-1+iD．-1-i
5．已知半径为120mm的圆上，有一条弧的长是144mm，则该弧所对的圆心角的弧度数为1.2．
15．给出下列三个命题：
①若回归直线的斜率估计值是1.23，样本点的中心为（4，5），则回归直线方程是$\widehaty=1.23x+0.08$；
②若偶函数f（x）（x∈R）满足f（x+1）=-f（x），且x∈[0，1]时，f（x）=x，则方程f（x）=log3|x|有3个根；
③已知函数f（x）=（$\frac{3}{2}$）x-sinx-1在[0，+∞）内只有两个零点．
正确命题的序号是①③（把你认为正确命题的序号都填上）
2．已知随机变量ξi满足P（ξi=1）=pi，P（ξi=0）=1-pi，i=1，2．若0＜p1＜p2＜$\frac{1}{2}$，则（　　）
A．E（ξ1）＜E（ξ2），D（ξ1）＜D（ξ2）B．E（ξ1）＜E（ξ2），D（ξ1）＞D（ξ2）C．E（ξ1）＞E（ξ2），D（ξ1）＜D（ξ2）D．E（ξ1）＞E（ξ2），D（ξ1）＞D（ξ2）
19．在直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=3cosθ}\\{y=sinθ}\end{array}\right.$，（θ为参数），直线l的参数方程为 $\left\{\begin{array}{l}{x=a+4t}\\{y=1-t}\end{array}\right.$，（t为参数）．
（1）若a=-1，求C与l的交点坐标；
（2）若C上的点到l距离的最大值为$\sqrt{17}$，求a．
20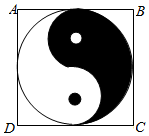．如图，正方形ABCD内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（　　）
A．$\frac{1}{4}$B．$\frac{π}{8}$C．$\frac{1}{2}$D．$\frac{π}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网