题目内容
如图,四边形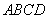 是正方形,
是正方形,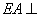 平面
平面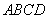 ,
,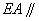
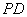 ,
,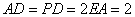 ,
,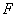 ,
,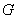 ,
, 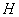 分别为
分别为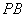 ,
,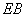 ,
,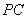 的中点.
的中点.
(Ⅰ)求证: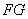
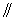 平面
平面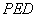 ;
;
(Ⅱ)求平面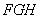 与平面
与平面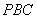 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)在线段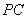 上是否存在一点
上是否存在一点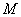 ,使直线
,使直线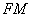 与直线
与直线
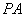 所成的角为
所成的角为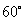 ?若存在,求出线段
?若存在,求出线段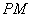 的长;若
的长;若
不存在,请说明理由.
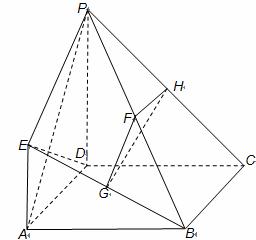
(Ⅰ)证明:因为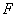 ,
,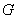 分别为
分别为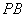 ,
, 的中点,
的中点,
所以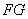
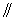
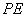 .
.
又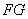
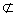 平面
平面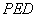 ,
,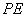
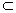 平面
平面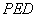 ,
,
所以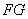
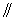 平面
平面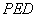 .
.
(Ⅱ)因为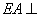 平面
平面 ,
,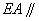
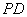 ,
,
 所以
所以 平面
平面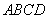 ,
,
所以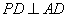 ,
,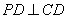 .
.
又因为四边形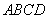 是正方形,
是正方形,
所以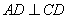 .
.
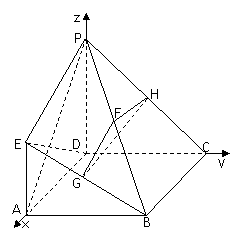
如图,建立空间直角坐标系,
因为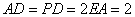 ,
,
所以
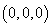 ,
,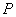
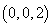 ,
,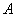
 ,
,
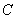
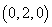 ,
,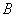
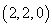 ,
,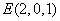 .
.
…………5分
因为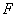 ,
,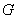 ,
, 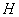 分别为
分别为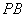 ,
,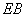 ,
,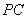 的中点,
的中点,
所以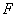
 ,
,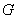
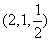 ,
,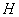
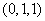 . 所以
. 所以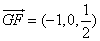 ,
, .
.
设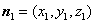 为平面
为平面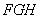 的一个法向量,则
的一个法向量,则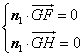 ,即
,即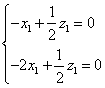 ,
,
再令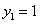 ,得
,得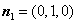 .
.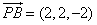 ,
,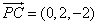 .
.
设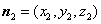 为平面
为平面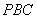 的一个法向量,则
的一个法向量,则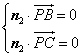 ,
,
即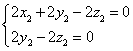 ,令
,令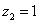 ,得
,得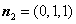 .
.
所以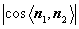 =
=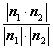 =
= .
.
所以平面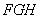 与平面
与平面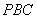 所成锐二面角的大小为
所成锐二面角的大小为 .
.
(Ⅲ)假设在线段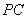 上存在一点
上存在一点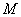 ,使直线
,使直线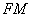 与直线
与直线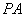 所成角为
所成角为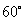 .
.
依题意可设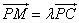 ,其中
,其中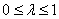 .
.
由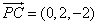 ,则
,则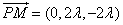 .
.
又因为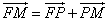 ,
,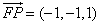 ,所以
,所以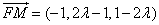 .
.
因为直线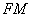 与直线
与直线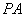 所成角为
所成角为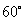 ,
,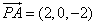 ,
,
所以 =
= ,即
,即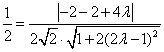 ,解得
,解得 .
.
所以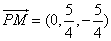 ,
,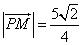 .
.
所以在线段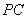 上存在一点
上存在一点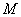 ,使直线
,使直线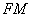 与直线
与直线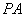 所成角为
所成角为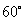 ,此时
,此时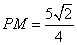 .
.

练习册系列答案
相关题目
 的前三项为
的前三项为 ,则这个数列的通项公式为 ( )
,则这个数列的通项公式为 ( ) B.
B. C.
C. D.
D.
 若对任意
若对任意 ,不等式
,不等式
 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 的渐近线与抛物线
的渐近线与抛物线 有公共点,则此双曲线的离心率的取值范围是
有公共点,则此双曲线的离心率的取值范围是 B.
B. C.
C. D.
D.
 于点
于点 经过圆心
经过圆心 ,则
,则 ,△
,△ 的面积是 .
的面积是 .
 ”是“直线
”是“直线 与直线
与直线 平行”的
平行”的 是虚数单位,那么
是虚数单位,那么 等于 .
等于 .  ,则判断框中可填入
,则判断框中可填入
 B.
B. C.
C. D.
D.
 ,则使函数
,则使函数 有零点的实数
有零点的实数 的取值范
的取值范 B.
B. C.
C. D.
D. 