题目内容
已知函数f(x+1)是偶函数,当1<x1<x2时,[f(x2)-f(x1)](x2-x1)>0恒成立,设a=f(-
),b=f(2),c=f(3),则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
考点:函数奇偶性的性质,函数恒成立问题
专题:函数的性质及应用
分析:根据条件求出函数f(x)在(1,+∞)上的单调性,然后根据函数f(x+1)是偶函数,利用单调性即可判定出a、b、c的大小.
解答:
解:解:∵当1<x1<x2时,[f(x2)-f(x1)](x2-x1)>0恒成立,
∴当1<x1<x2时,f (x2)-f (x1)>0,
即f (x2)>f (x1),
∴函数f(x)在(1,+∞)上为单调增函数,
∵f(1+x)=f(1-x),
∴函数f(x)关于x=1对称,
∴a=f(-
)=f(
),
又函数f(x)在(1,+∞)上为单调增函数,
∴f(2)<f(
)<f(3),
即f(2)<f(-
)=<f(3),
∴a,b,c的大小关系为b<a<c.
故选:A.
∴当1<x1<x2时,f (x2)-f (x1)>0,
即f (x2)>f (x1),
∴函数f(x)在(1,+∞)上为单调增函数,
∵f(1+x)=f(1-x),
∴函数f(x)关于x=1对称,
∴a=f(-
| 1 |
| 2 |
| 5 |
| 2 |
又函数f(x)在(1,+∞)上为单调增函数,
∴f(2)<f(
| 5 |
| 2 |
即f(2)<f(-
| 1 |
| 2 |
∴a,b,c的大小关系为b<a<c.
故选:A.
点评:本题考查了函数性质的应用,主要考查了函数单调性的判断以及运用单调性比较函数值的大小,同时考查了函数的对称性的应用,是函数性质的一个综合考查.属于基础题.

练习册系列答案
相关题目
若函数y=ax+b的部分图象如图所示,则( )
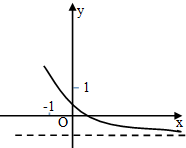

| A、0<a<1,-1<b<0 |
| B、0<a<1,0<b<1 |
| C、a>1,-1<b<0 |
| D、a>1,0<b<1 |
已知直线a,b,平面α,β,且a⊥α,b?β,则“a⊥b”是“α∥β”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若U={1,2,3,4,5,6,},M={1,2,5},则∁UM=( )
| A、{2,4} |
| B、{1,3,6} |
| C、{3,5} |
| D、{3,4,6} |
如果|
|=|
|=1,
与
的夹角为θ,
•
=
,则θ=( )
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| A、90° | B、30° |
| C、60° | D、120° |
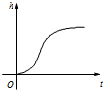
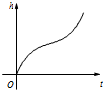
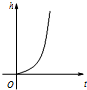
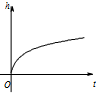
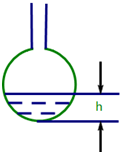 匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )
匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )