题目内容
定义在R上的奇函数f(x)的最小正周期为4,且在[2,3]上是增函数,有下列命题:
①f(2014)=0;②f(2015)>0;③f(
)>0;④f(
)<f(
).
正确命题的个数为( )
①f(2014)=0;②f(2015)>0;③f(
| 2x2+4x+5 |
| x2+2x+2 |
| 2015 |
| 2014 |
| 5 |
| 2 |
正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:运用奇函数的定义和周期函数的定义,可令x=-2,可得f(2)=0,且f(0)=0,运用周期为4,即可判断①;再由单调性,即可判断②;化简分式可得2<2+
<3,由单调性即可判断③;再由条件可得f(4-x)=f(-x)=-f(x),结合单调性,可得f(
)<0,f(
)>0,即可判断④.
| 1 |
| x2+2x+2 |
| 2015 |
| 2014 |
| 5 |
| 2 |
解答:
解:定义在R上的奇函数f(x)的最小正周期为4,则f(x+4)=f(x),
f(0)=0,f(-2)=f(2)=-f(2),即有f(2)=0,
对于①,f(2014)=f(503×4+2)=f(2)=0,则①对;
对于②,f(2015)=f(503×4+3)=f(3),由于f(x)在[2,3]上是增函数,
则f(3)>f(2)=0,则②对;
对于③,f(
)=f(2+
),由于x2+2x+2=(x+1)2+1≥1,
则2<2+
<3,由f(x)在[2,3]上是增函数,则f(
)>f(2)=0,则③对;
对于④,由f(-x)=-f(x),f(x+4)=f(x),则f(4-x)=f(-x)=-f(x),
则f(
)=-f(4-
)=-f(
),由2<
<3,则f(
)>f(2)=0,
则f(
)<0,由2<
<3,则f(
)>0,则f(
)<f(
),则④对.
则①②③④都对.
故选D.
f(0)=0,f(-2)=f(2)=-f(2),即有f(2)=0,
对于①,f(2014)=f(503×4+2)=f(2)=0,则①对;
对于②,f(2015)=f(503×4+3)=f(3),由于f(x)在[2,3]上是增函数,
则f(3)>f(2)=0,则②对;
对于③,f(
| 2x2+4x+5 |
| x2+2x+2 |
| 1 |
| x2+2x+2 |
则2<2+
| 1 |
| x2+2x+2 |
| 2x2+4x+5 |
| x2+2x+2 |
对于④,由f(-x)=-f(x),f(x+4)=f(x),则f(4-x)=f(-x)=-f(x),
则f(
| 2015 |
| 2014 |
| 2015 |
| 2014 |
| 6041 |
| 2014 |
| 6041 |
| 2014 |
| 6041 |
| 2014 |
则f(
| 2015 |
| 2014 |
| 5 |
| 2 |
| 5 |
| 2 |
| 2015 |
| 2014 |
| 5 |
| 2 |
则①②③④都对.
故选D.
点评:本题考查函数的奇偶性和单调性以及周期性的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知{an}是由正数组成的数列,其前n项和Sn与an之间满足:an+
=
(n≥1且n∈N*).
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=(
)nan,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
2Sn+
|
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=(
| 1 |
| 2 |
关于x的不用等式ax+b>0的解集为(-∞,1),则关于x的不等式(bx-a)(x+2)>0的解集为( )
| A、(-2,1) |
| B、(-∞,-2)∪(-1,+∞) |
| C、(-2,-1) |
| D、(-∞,-2)∪(1,+∞) |
要得到函数y=cos(2x+
)的图象,只需将函数y=cos2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
已知平面直角坐标系中三个点A(0,2),B(-1,-2),C(3,1),且
=2
,则向量
的坐标为( )
| BC |
| AD |
| CD |
A、(2,
| ||
B、(1,-
| ||
C、(-1,
| ||
| D、(3,1) |
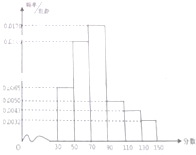 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: