题目内容
已知平面直角坐标系中三个点A（0，2），B（-1，-2），C（3，1），且
=2
，则向量
的坐标为（ ）
| BC |
| AD |
| CD |
A、（2，
| ||
B、（1，-
| ||
C、（-1，
| ||
| D、（3，1） |
考点：平面向量的坐标运算
专题：平面向量及应用
分析：设出D的坐标，利用向量相等，求出D的坐标，然后求解向量
的坐标．
| CD |
解答：
解：设D（a，b），A（0，2），B（-1，-2），C（3，1），则
=（4，3），2
=（2a，2b-4），
∵
=2
，∴4=2a，3=2b-4，
解得：a=2，b=
，
向量
=（2，
）．
故选：A．
| BC |
| AD |
∵
| BC |
| AD |
解得：a=2，b=
| 7 |
| 2 |
向量
| CD |
| 7 |
| 2 |
故选：A．
点评：本题考查向量的坐标运算，向量的相等，考查计算能力．
练习册系列答案
相关题目
定义在R上的奇函数f（x）的最小正周期为4，且在[2，3]上是增函数，有下列命题：
①f（2014）=0；②f（2015）＞0；③f（
）＞0；④f（
）＜f（
）．
正确命题的个数为（ ）
①f（2014）=0；②f（2015）＞0；③f（
| 2x2+4x+5 |
| x2+2x+2 |
| 2015 |
| 2014 |
| 5 |
| 2 |
正确命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
若角α和角β的终边关于x轴对称，则角α可以用角β表示为（ ）
| A、K•360°+β（k∈Z） |
| B、K•360°-β（k∈Z） |
| C、K•180°+β（k∈Z） |
| D、K•180°-β（k∈Z） |
计算lg
+
lg5的结果为（ ）
| 2 |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、0 | ||
| D、1 |
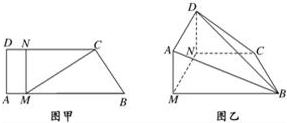如图甲，直角梯形ABCD中，AB∥CD，∠ADC=90°，点M，N分别在线段AB、CD上，且MN⊥AB，BC=1，MB=2，∠CBM=60°，若梯形ABCD沿MN折起，使DN⊥NC，如图乙．