题目内容

已知函数
（I）若，判断函数在定义域内的单调性；
（II）若函数在内存在极值，求实数m的取值范围。

（I）当单调递增；
当单调递减。
（II）

解析试题分析：（I）显然函数定义域为（0，+）若m=1，
由导数运算法则知
令    
当单调递增；
当单调递减。   
（II）由导数运算法则知，
令   
当单调递增；
当单调递减。  
故当有极大值，根据题意
   
考点：函数在某点取得极值的条件；利用导数研究函数的单调性．．
点评：本题主要考查函数的导数与单调区间，极值的关系，求单调区间时，注意单调区间是定义域的子区间

练习册系列答案
相关题目

已知函数（e为自然对数的底数）．
（Ⅰ）当时，求函数的单调区间；
（Ⅱ）若对于任意，不等式恒成立，求实数t的取值范围．

已知f（x）=1nx－a（x－l），a∈R
（I）讨论f（x）的单调性；
（Ⅱ）若x≥1时，石恒成立，求实数a的取值范围，

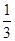已知函数f(x)＝－x3＋x2－2x(a∈R)．
(1)当a＝3时，求函数f(x)的单调区间；
(2)若对于任意x∈[1，＋∞)都有f′(x)<2(a－1)成立，求实数a的取值范围；
(3)若过点可作函数y＝f(x)图象的三条不同切线，求实数a的取值范围．

若函数．当时，函数取得极值．
（1）求函数的解析式；
（2）若函数有3个解，求实数的取值范围．

已知函数在与时都取得极值
(1)求的值与函数的单调区间
(2)若对，不等式恒成立，求c的取值范围

已知，为的导函数.
（Ⅰ）若，求的值；
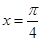（Ⅱ）若图象与图象关于直线对称，△ABC的三个内角A、B、C所对的边长分别为，角A为的初相，，求△ABC面积的最大值.

已知函数
（1）当时，求的极小值；
（2）若直线对任意的都不是曲线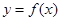的切线，求的取值范围；
（3）设，求的最大值的解析式．

设函数
（1）若函数在x=1处与直线相切．
①求实数，的值；②求函数在上的最大值.
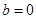（2）当时，若不等式对所有的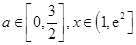都成立，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网