题目内容
已知 ,
, 为
为 的导函数.
的导函数.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)若 图象与
图象与 图象关于直线
图象关于直线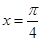 对称,△ABC的三个内角A、B、C所对的边长分别为
对称,△ABC的三个内角A、B、C所对的边长分别为 ,角A为
,角A为 的初相,
的初相, ,求△ABC面积的最大值.
,求△ABC面积的最大值.
(Ⅰ)
 ;
;
(Ⅱ) .
.
解析试题分析:(Ⅰ) 1分
1分
依题意: ∴
∴ 2分
2分
∴ 5分
5分 6分
6分
(Ⅱ)
 8分
8分
初相为 ,∴
,∴ 9分
9分 ,即
,即  10分
10分
又 (等号成立条件是
(等号成立条件是 )
)
∴ ∴
∴ 11分
11分
∴ 12分
12分
考点:导数计算,和差倍半的三角函数公式,三角函数的图象和性质,余弦定理的应用,基本不等式的应用。
点评:中档题,涉及三角函数图象和性质的研究,往往需要首先利用“三角公式”实现“化一”。本题运用余弦定理,建立了a,b,c的关系式,应用“基本不等式”确定三角形面积的最值。综合性较强,也比较典型。

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

 在
在 上的最大值和最小值.
上的最大值和最小值. 作曲线
作曲线 的切线,求此切线的方程.
的切线,求此切线的方程. 

 恒成立?若存在,求出a的取值条件;
恒成立?若存在,求出a的取值条件;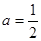 时,求证:f(1)+f(2)+f(3)+…+
时,求证:f(1)+f(2)+f(3)+…+ .
.
 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性; 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。
 能否在
能否在 处取得极值,请说明理由;
处取得极值,请说明理由; ,当
,当 时,函数
时,函数 的图像有两个公共点,求
的图像有两个公共点,求 的取值范围.
的取值范围. 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。 的值;
的值; 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又 .
. 的解析式;
的解析式; (m>0)上恒有
(m>0)上恒有
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围。
的取值范围。 .(
.( )
) 时,试确定函数
时,试确定函数 在其定义域内的单调性;
在其定义域内的单调性; 上的最小值;
上的最小值; .
.