题目内容
设函数
(1)若函数 在x=1处与直线
在x=1处与直线 相切.
相切.
①求实数 ,
, 的值;②求函数
的值;②求函数 在
在 上的最大值.
上的最大值.
(2)当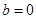 时,若不等式
时,若不等式 对所有的
对所有的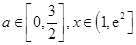 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
(1)① ②
② (2)
(2)
解析试题分析:(1)① ,
, 函数
函数 在
在 处与直线
处与直线 相切,
相切, 解得
解得
②
当 时,令
时,令 得
得 ;
;
令 ,得
,得
 在
在 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减, (6分)
(6分)
(2)当b=0时,
若不等式 对所有的
对所有的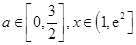 都成立,
都成立,
则 对所有的
对所有的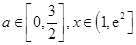 都成立,
都成立,
即 对所有的
对所有的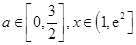 都成立,
都成立,
令 为一次函数,
为一次函数,

 在
在 上单调递增
上单调递增 ,
, 对所有的
对所有的 都成立
都成立
 . (14分)
. (14分)
考点:利用函数导数求最值及求解不等式恒成立问题
点评:求最值的步骤:定义域内求导,求得单调区间,确定极值最值,关于含参不等式恒成立问题常用的转化思路是将参数分离,构造新函数,从而通过新函数的最值求得参数范围

练习册系列答案
相关题目

 ,判断函数在定义域内的单调性;
,判断函数在定义域内的单调性; 内存在极值,求实数m的取值范围。
内存在极值,求实数m的取值范围。
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围。
的取值范围。 ,
, ,求函数
,求函数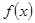 的极小值,
的极小值, ,设
,设 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.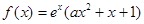 ,
,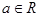 ;
; 的单调性;
的单调性; 上的最大值为
上的最大值为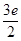 ,求
,求 的值.
的值. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.求
平行.求 .(
.( )
) 时,试确定函数
时,试确定函数 在其定义域内的单调性;
在其定义域内的单调性; 上的最小值;
上的最小值; .
.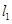 与直线4x-y-1=0平行,且点 P0 在第三象限,
与直线4x-y-1=0平行,且点 P0 在第三象限,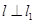 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.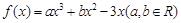 ,且
,且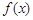 在
在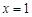 和
和 处取得极值.
处取得极值. ,是否存在实数
,是否存在实数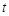 ,使得曲线
,使得曲线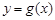 与
与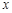 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出