题目内容
17.函数f(x)=$\sqrt{|x+1|+|x+2|-5}$.(1)求函数f(x)的定义域A;
(2)设B={x|-1<x<2},当实数a、b∈(B∩∁RA)时,证明:$\frac{|a+b|}{2}<|1+\frac{ab}{4}$|.
分析 (1)分类讨论x的范围,根据负数没有平方根,利用绝对值的代数意义求出x的范围,即可确定出A;
(2)求出B与A补集的交集,得到a、b满足的集合,把所证等式两边平方,利用作差法验证即可.
解答 (1)解:由题意得:|x+1|+|x+2|-5≥0,
当x≤-2时,得x≤-4;当-2<x<-1时,无解;当x≥-1时,得x≥1,
∴A={x|x≤-4或x≥1};
(2)证:∵B={x|-1<x<2},∁RA={x|-4<x<1},
∴B∩∁RA={x|-1<x<1},
∴a、b∈{x|-1<x<1},
要证$\frac{|a+b|}{2}$<|1+$\frac{ab}{4}$|,只需证4(a+b)2<(4+ab)2,
∵4(a+b)2-(4+ab)2=4a2+4b2-a2b2-16=(b2-4)(4-a2),
∵a、b∈{ x|-1<x<1},
∴(b2-4)(4-a2)<0,
∴4(a+b)2<(4+ab)2,
∴$\frac{|a+b|}{2}$<|1+$\frac{ab}{4}$|成立.
点评 此题考查了交、并、补集的混合运算,以及函数的定义域及其求法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知抛物线的顶点在坐标原点,焦点是圆(x-3)2+y2=4的圆心,则抛物线的方程是( )
| A. | x2=12y | B. | x2=6y | C. | y2=12x | D. | y2=6x |
9.执行下图的程序框图,若输入的a,b,k分别是2,1,3,则输出的M=( )
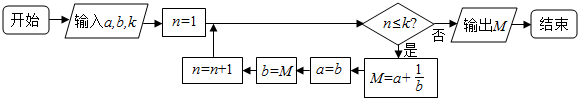
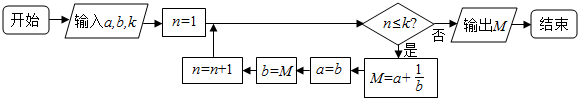
| A. | $\frac{4}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
7.已知函数f(x)=-x3+6x2-9x+8,则过点(0,0)可以作几条直线与曲线y=f(x)相切( )
| A. | 3条 | B. | 1条 | C. | 0条 | D. | 2条 |
