题目内容
已知等比数列{an}中,a1=2,S3=6,则公比q的值为 .
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:首先根据等比数列的前n项和公式,把题中的已知条件代入Sn=
(q≠1)公式求的结果.
| a1(1-qn) |
| 1-q |
解答:
解:在等比数列{an}中,Sn=
(q≠1)
∵a1=2,S3=6
q2+q-2=0
解得:q=-2或1
故答案为:q=-2或1
| a1(1-qn) |
| 1-q |
∵a1=2,S3=6
q2+q-2=0
解得:q=-2或1
故答案为:q=-2或1
点评:本题考查的知识点:等比数列的前n项和公式及相关的运算问题.

练习册系列答案
相关题目
已知函数f(x)=sin2x向左平移
个单位后,得到函数y=g(x),下列关于y=g(x)的说法正确的是( )
| π |
| 6 |
A、图象关于点(-
| ||||
B、图象关于x=-
| ||||
C、在区间[-
| ||||
D、在[-
|
若f(x)=ax2-
,a为一个正常数,且f(f(
))=-
,那么a的值为( )
| 2 |
| 2 |
| 2 |
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
若集合A={0,1,2,3,4},B={1,2,4}则A∪B=( )
| A、{0,1,2,3,4} |
| B、{1,2,3,4} |
| C、{1,2} |
| D、{0} |
M是椭圆
+
=1上的点,F1、F2是椭圆的两个焦点,∠F1MF2=60°,则△F1MF2的面积等于( )
| x2 |
| 25 |
| y2 |
| 9 |
A、3
| ||
B、6
| ||
| C、3 | ||
D、2
|
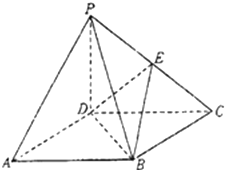 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.