题目内容

10．某几何体的三视图如图所示，则该几何体的表面积为（　　）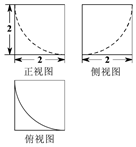
A．$8-\frac{4}{3}π$B．$8-\frac{2}{3}π$C．24-πD．24+π

分析 由已知三视图得到几何体的形状，然后计算体积．

解答 解：由已知三视图得到几何体是一个正方体割去半径为2的$\frac{1}{8}$个球，
所以表面积为$2×2×6-\frac{3}{4}π×{2}^{2}+\frac{1}{8}×4π×{2}^{2}$=24-π；
故选：C．

点评 本题考查了由几何体的三视图求几何体的表面积；关键是正确还原几何体．

练习册系列答案
相关题目
20．$y=sin（{ωx+\frac{5π}{6}}）（{0＜ω＜π}）$的图象与坐标轴的所有交点中，距离原点最近的两个点为$（{0，\frac{1}{2}}）$和$（{\frac{1}{2}，0}）$，那么该函数图象的所有对称轴中，距离y轴最近的一条对称轴是（　　）
A．x=-1B．$x=-\frac{1}{2}$C．x=1D．$x=\frac{3}{2}$
1．将4个不同的小球装入4个不同的盒子，则在至少一个盒子为空的条件下，恰好有两个盒子为空的概率是$\frac{21}{58}$．
18．计算  $\int_0^2{|1-x|dx}$．
5．一个四棱锥的三视图在1×1的方格中显示如图，则此几何体的体积为（　　）
A．8B．4C．3D．$\frac{8}{3}$
15．在△ABC中，A=60°，b=1，面积为$\sqrt{3}$，则$\frac{a+2b-3c}{sinA+2sinB-3sinC}$=$\frac{{2\sqrt{39}}}{3}$．
2．圆${C_1}：{（x+2）^2}+{（y-m）^2}=9$与圆${C_2}：{（x-m）^2}+{（y+1）^2}=4$外切，则m的值0或-3．
19．已知θ的终边过点（2，a），且$tan（\frac{π}{4}-θ）=-3$，则a=-4．
20．已知一个几何体的三视图如图所示（单位：m），其中俯视图为正三角形，则该几何体的体积为$\frac{4\sqrt{3}}{3}$m3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网