题目内容
2．圆${C_1}：{（x+2）^2}+{（y-m）^2}=9$与圆${C_2}：{（x-m）^2}+{（y+1）^2}=4$外切，则m的值0或-3．分析 由题意，圆心距=$\sqrt{（m+2）^{2}+（-1-m）^{2}}$=5，即可求出m的值．
解答 解：由题意，圆心距=$\sqrt{（m+2）^{2}+（-1-m）^{2}}$=5，
∴m=0或-3，
故答案为0或-3．
点评 本题考查圆与圆的位置关系，考查方程思想，比较基础．
练习册系列答案
相关题目
13．已知m，n是两条不同直线，α，β是两个不同平面，则下列命题中假命题的是（ ）
| A． | 若m⊥α，m⊥β则α∥β | B． | 若m∥n，m⊥α，则n⊥α | ||
| C． | 若m∥α，α∩β=n，则m∥n | D． | 若m⊥α，m?β则 α⊥β |
10．某几何体的三视图如图所示，则该几何体的表面积为（ ）
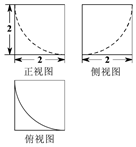
| A． | $8-\frac{4}{3}π$ | B． | $8-\frac{2}{3}π$ | C． | 24-π | D． | 24+π |
14．一个几何体的三视图如图所示，则该几何体的表面积为（ ）
| A． | $\frac{3π}{2}$+1+$\frac{\sqrt{3}}{2}$ | B． | 3π+$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | C． | $\frac{3π+1+\sqrt{3}}{2}$ | D． | 3π+1+$\frac{\sqrt{3}}{2}$ |
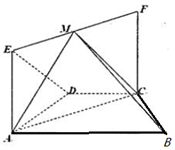如图，在等腰梯形ABCD中，AB∥CD，AD=DC=CB=2，∠ABC=60°，四边形ACFE为矩形，CF=$\sqrt{3}$，平面ACFE⊥平面ABCD，点M为线段EF中点．