题目内容
已知O为平面直角坐标系的原点,过点M(-2,0)的直线l与圆x +y
+y =1交于P、Q两点,且
=1交于P、Q两点,且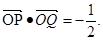
(Ⅰ)求∠PDQ的大小;
(Ⅱ)求直线l的方程.
(Ⅰ)∠POQ=120°.(Ⅱ)  或
或 .
.
解析试题分析:(Ⅰ)因为P、Q两点在圆x +y
+y =1上,所以
=1上,所以 ,
,
因为 ,
,
所以 .
.
所以∠POQ=120°. 5分
(Ⅱ)依题意,直线l的斜率存在,
因为直线l过点M(-2,0),可设直线l:y=k(x+2).
由(Ⅰ)可知O到直线l的距离等于 .
.
所以
得
所以直线 的方程为
的方程为 或
或 9分
9分
考点:直线与圆的位置关系,直线方程,平面向量的数量积。
点评:中档题,中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。恰当的运用圆中的“特征三角形”,转化成点到直线的距离问题,更为简洁。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知数列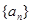 的前
的前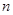 项和为
项和为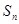 ,且
,且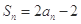 则
则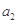 等于( )
等于( )
| A.4 | B.2 | C.1 | D.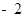 |
数列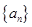 中,已知对任意正整数
中,已知对任意正整数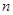 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
在各项均为正数的数列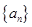 中,对任意
中,对任意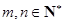 都有
都有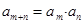 .若
.若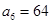 ,
,
则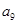 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
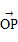 =
=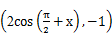 ,
,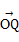 =
=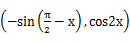 ,定义函数f(x)=
,定义函数f(x)= ,点
,点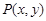 为直线
为直线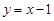 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求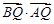 的值.
的值. 是函数
是函数 ,
, )一个周期内图象上的两点,函数
)一个周期内图象上的两点,函数 的图象与
的图象与 轴交于点
轴交于点 ,满足
,满足 .
. 在区间
在区间 内的零点.
内的零点. 的圆心
的圆心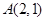 关于直线
关于直线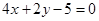 对称,圆
对称,圆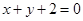 相切.
相切.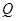 为圆
为圆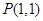 ,
,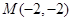 ,求
,求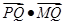 的最小值;
的最小值;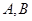 ,且直线
,且直线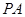 和直线
和直线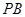 的倾斜角互补,
的倾斜角互补,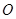 为坐标原点,试判断直线
为坐标原点,试判断直线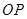 和
和 是否平行?请说明理由.
是否平行?请说明理由. ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.