题目内容
已知圆 的圆心
的圆心 与点
与点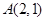 关于直线
关于直线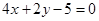 对称,圆
对称,圆 与直线
与直线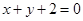 相切.
相切.
(1)设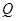 为圆
为圆 上的一个动点,若点
上的一个动点,若点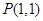 ,
,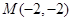 ,求
,求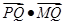 的最小值;
的最小值;
(2)过点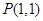 作两条相异直线分别与圆
作两条相异直线分别与圆 相交于
相交于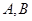 ,且直线
,且直线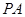 和直线
和直线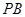 的倾斜角互补,
的倾斜角互补,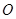 为坐标原点,试判断直线
为坐标原点,试判断直线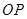 和
和 是否平行?请说明理由.
是否平行?请说明理由.
(1)-4;(2)直线 和
和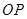 一定平行.
一定平行.
解析试题分析:本题主要考查圆的标准方程和几何性质、直线的方程、向量的点乘、平面内两点间距离公式、点到直线的距离等基础知识.考查数形结合的数学思想.考查运算求解能力、综合分析和解决问题的能力.第一问,利用两个点关于直线对称,列出方程组,解出 ,即得到圆心坐标,再利用点到直线的距离求半径,写出圆的方程,利用向量的点乘列出式子,数形结合找出最小值;第二问,利用直线与圆的位置关系列出方程,得出
,即得到圆心坐标,再利用点到直线的距离求半径,写出圆的方程,利用向量的点乘列出式子,数形结合找出最小值;第二问,利用直线与圆的位置关系列出方程,得出 两点的横坐标,利用斜率公式写出式子,判断两个斜率是否相等.
两点的横坐标,利用斜率公式写出式子,判断两个斜率是否相等.
试题解析:(Ⅰ)设圆心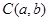 ,则
,则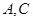 中点坐标为
中点坐标为 , 1分
, 1分
∵圆心 与点
与点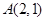 关于直线
关于直线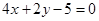 对称,
对称,
∴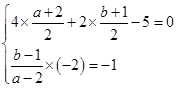 ,解得
,解得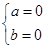 , 3分
, 3分
∴圆心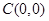 到直线
到直线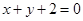 的距离
的距离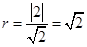 , 4分
, 4分
∴求圆 的方程为
的方程为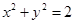 . 5分
. 5分
设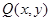 ,则
,则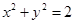 ,
,
∴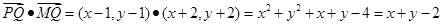 , 6分
, 6分
作直线 :
: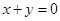 ,向下平移此直线,当与圆
,向下平移此直线,当与圆 相切时
相切时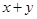 取得最小值,这时切点坐标为
取得最小值,这时切点坐标为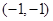 ,
,
所以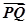 ·
·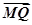 的最小值为-4. 8分
的最小值为-4. 8分
(Ⅱ)由题意知,直线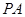 和直线
和直线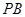 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设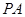 :
: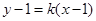 ,
,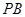 :
: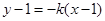 ,由
,由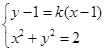 ,得
,得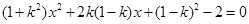 .
.
因为点 的横坐标
的横坐标 一定是该方程的解,故可得
一定是该方程的解,故可得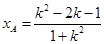 ,同理,
,同理,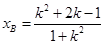 ,
,
则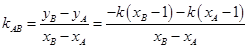
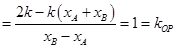 .
.
所以,直线 和
和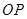 一定平行. 14分
一定平行. 14分
考点:1.中点坐标公式;2.点到直线的距离;3.向量的点乘;4.斜率的公式;5.直线与圆的位置关系.

 名校课堂系列答案
名校课堂系列答案已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-ka+ b,m∈R,k、t为正实数.
b,m∈R,k、t为正实数.
(1)若a∥b,求m的值;
(2)若a⊥b,求m的值;
(3)当m=1时,若x⊥y,求k的最小值.
已知数列:2,0,2,0,2,0, .前六项不适合下列哪个通项公式
A. =1+(―1)n+1 =1+(―1)n+1 | B. =2|sin =2|sin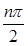 | | |
C. =1-(―1)n =1-(―1)n | D. =2sin =2sin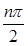 |
 =2a-b,
=2a-b, =3a+b,
=3a+b,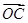 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线;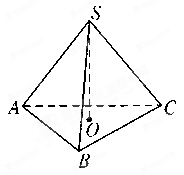
 (;(2)
(;(2)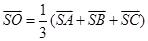 .
. ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线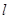 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 +y
+y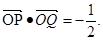
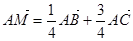 ,则
,则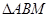 与
与 的面积之比为 .
的面积之比为 . 个点,相应的图案中总的点数记为
个点,相应的图案中总的点数记为 ,则
,则 +
+ +
+ + …… +
+ …… + =( )
=( )



