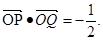题目内容
已知向量 ,
, 设函数
设函数 .
. 求
求 的最小正周期与单调递增区间;
的最小正周期与单调递增区间; 在
在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, ,求
,求 的最大值.
的最大值.

 的最小正周期
的最小正周期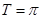 ,单调递增区间为
,单调递增区间为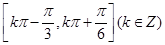 ;
;
 最大为
最大为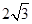 .
.
解析试题分析: 利用向量数量积的坐标运算及三角恒等变换得到
利用向量数量积的坐标运算及三角恒等变换得到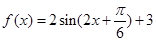 ,可得最小正周期为
,可得最小正周期为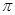 .利用复合函数的单调性得单调递增区间
.利用复合函数的单调性得单调递增区间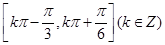
 先由
先由 计算出
计算出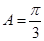 ,所以
,所以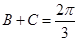 .又
.又 ,由正弦定理推出
,由正弦定理推出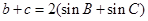
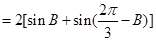
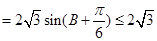 .或者由余弦定理得
.或者由余弦定理得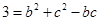 ,再由基本不等式得
,再由基本不等式得 的最大值为
的最大值为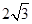 .
.
试题解析:(Ⅰ)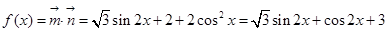
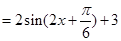 3分
3分
∴ 的最小正周期
的最小正周期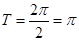 4分
4分
由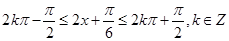 得
得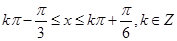
∴ 的单调递增区间为
的单调递增区间为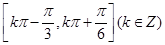 6分
6分
(Ⅱ)由 得
得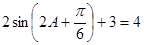 ,
,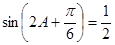
∵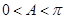 ∴
∴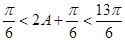 ∴
∴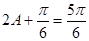 ,
,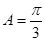 8分
8分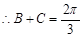
法一:又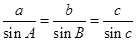 ,
,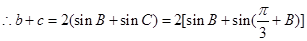
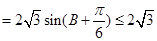
∴当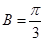 时,
时, 最大为
最大为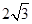 12分
12分
法二: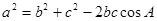 即
即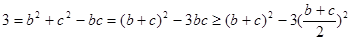
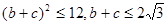 ;当且仅当
;当且仅当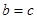 时等号成立. 12分
时等号成立. 12分
考点:1.平面向量的坐标运算;2.三角恒等变换;3.解三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}满足an = nkn(n∈N*,0 < k < 1),下面说法正确的是( )
①当 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当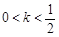 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当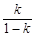 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
| A.①② | B.②④ | C.③④ | D.②③ |
数列 ,3,
,3, ,
, ,
, ,…,则9是这个数列的第( )
,…,则9是这个数列的第( )
| A.12项 | B.13项 | C.14项 | D.15项 |
数列1,2,4,8,16,32,…的一个通项公式是( )
| A.an=2n-1 | B.an= | C.an= | D.an= |
[2013·江西抚州月考]数列{an}的前n项积为n2,那么当n≥2时,{an}的通项公式为( )
| A.an=2n-1 | B.an=n2 |
C.an= | D.an= |
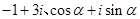 (
(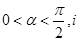 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为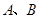 ,点
,点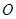 是坐标原点.
是坐标原点. ,求
,求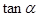 的值;
的值; 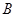 点的横坐标为
点的横坐标为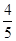 ,求
,求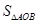 .
. +
+ +
+ =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形. 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
. 的值;
的值; ,
, ,求角
,求角 的大小及向量
的大小及向量 在
在 方向上的投影.
方向上的投影. +y
+y