题目内容
设函数y=2sin（
-
）（0≤x≤9）的最大值为a，最小值为b，求a-b的值．
| πx |
| 6 |
| π |
| 3 |
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：求出角的取值范围，结合正弦函数的单调性进行求解即可．
解答：
解：∵0≤x≤9，
∴0≤
≤
，
-
≤
-
≤
，
∴当
-
=
时，函数取得最大值2，
当
-
=-
时，函数取得最小值2sin（-
）=-
×2=-
，
即a=2，b=-
，
则a-b=2-（-
）=2+
．
∴0≤
| πx |
| 6 |
| 3π |
| 2 |
-
| π |
| 3 |
| πx |
| 6 |
| π |
| 3 |
| 7π |
| 6 |
∴当
| πx |
| 6 |
| π |
| 3 |
| π |
| 2 |
当
| πx |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 3 |
即a=2，b=-
| 3 |
则a-b=2-（-
| 3 |
| 3 |
点评：本题主要考查三角函数的最值的求解，根据角的求值范围结合三角函数的单调性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知命题p：a≠1或b≠2，命题q：a+b≠3，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列说法不正确的是（ ）
| A、“若a+b≥2，则a，b中至少有一个不小于1”的逆命题为真 |
| B、存在正实数a，b，使得lg（a+b）=1ga+1gb |
| C、命题p：?x∈R，使得x2+x-1＜0，则￢p：?x∈R，使得x2+x-1≥0 |
| D、a+b+c=0是方程ax2+bx+c=0（a≠0）有一个根为1的充分必要条件 |
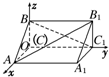如图所示，在空间直角坐标系中有直三棱柱ABCA1B1C1，CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为
如图，抛物线y=ax2-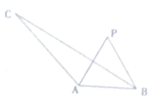
如图所示，在△ABC中，∠BAC=120°，AC=3，AB=1，P为∠BAC平分线上异于A的一点，∠APB=α，三角形PAB的面积记为S．