题目内容
14.若集合P={x||x|<3,且x∈Z},Q={x|x(x-3)≤0,且x∈N},则P∩Q等于( )| A. | {0,1,2} | B. | {1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
分析 化简集合P、Q,求出P∩Q即可.
解答 解:P={x||x|<3,且x∈Z}={x|-3<x<3,x∈Z}={-2,-1,0,1,2},
Q={x|x(x-3)≤0,且x∈N}={x|0≤x≤3,且x∈N}={0,1,2,3},
∴P∩Q={0,1,2}.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
相关题目
4.已知P为椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$上的点,点M为圆${C_1}:{(x+3)^2}+{y^2}=1$上的动点,点N为圆C2:(x-3)2+y2=1上的动点,则|PM|+|PN|的最大值为( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
5.已知向量$\overrightarrow{a}$=(cosα,-2),$\overrightarrow{b}$=(sinα,1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则2snαcosα等于( )
| A. | -$\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{{5}_{\;}}$ |
2.某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 分数区间 | 甲班频率 | 乙班频率 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.3 |
| [90,120) | 0.2 | 0.2 |
| [120,150) | 0.2 | 0.1 |
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
| 优秀 | 不优秀 | 总计 | |
| 甲班 | |||
| 乙班 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
6.随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,宜城各医院产科就已经是一片忙碌,至今热度不减.卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中20个是“二孩”宝宝;市妇幼保健院共有30个猴宝宝降生,其中10个是“二孩”宝宝.
(I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
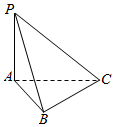 如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.
如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.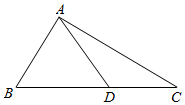 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.