题目内容
13．已知抛物线的标准方程为x2=4y，则下列说法正确的是（ ）| A． | 开口向左，准线方程为x=1 | B． | 开口向右，准线方程为x=-1 | ||
| C． | 开口向上，准线方程为y=-1 | D． | 开口向下，准线方程为y=1 |
分析 根据抛物线的标准方程得到焦点在y轴上以及2p=4，即可得出结论．
解答 解：因为抛物线的标准方程为：x2=4y，焦点在y轴上；
所以：2p=4，即p=2，
所以准线方程y=-1，开口向上．
故选：C．
点评 本题主要考查抛物线的基本性质．解决抛物线的题目时，一定要先判断焦点所在位置．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4．向量$\overrightarrow{e_1}，\;\overrightarrow{e_2}，\;\overrightarrow a，\;\overrightarrow b$在正方形网格中的位置如图所示，则$\overrightarrow a-\overrightarrow b$=（ ）
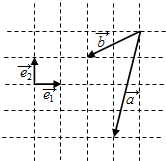
| A． | $-4\overrightarrow{e_1}-2\overrightarrow{e_2}$ | B． | $-2\overrightarrow{e_1}-4\overrightarrow{e_2}$ | C． | $\overrightarrow{e_1}-3\overrightarrow{e_2}$ | D． | $3\overrightarrow{e_1}-\overrightarrow{e_2}$ |
1．已知$sin（π+α）=-\frac{1}{2}$，那么$cos（\frac{3}{2}π+α）$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
8．若实数x，y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$，则z=x-2y的最小值为（ ）
| A． | -7 | B． | -3 | C． | 1 | D． | 9 |
18．设函数$f（x）={e^{{x^2}-3x}}$（e为自然底数），则使f（x）＜1成立的一个充分不必要条件是（ ）
| A． | 0＜x＜1 | B． | 0＜x＜4 | C． | 0＜x＜3 | D． | 3＜x＜4 |