题目内容


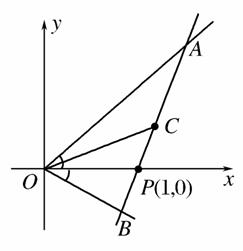
如图，射线OA、OB分别与x轴正半轴成45°和30°角，过点P(1,0)作直线AB分别交OA、OB于A、B两点，当AB的中点C恰好落在直线y＝x上时，求直线AB的方程．


解：由题意可得kOA＝tan 45°＝1，

kOB＝tan(180°－30°)＝－，

所以直线lOA：y＝x，lOB：y＝－x.

设A(m，m)，B(－n，n)，

所以AB的中点C，

由点C在y＝x上，且A、P、B三点共线得


练习册系列答案
相关题目

数列{an}的通项公式是an＝n2－7n＋6.

(1)这个数列的第4项是多少？

(2)150是不是这个数列的项？若是这个数列的项，它是第几项？

(3)该数列从第几项开始各项都是正数？

数列{an}的前n项和为Sn，且a1＝1，an＋1＝3Sn(n＝1,2,3，…)，则log4S10＝________.

一学生参加市场营销调查活动，从某商场得到11月份新款家电M的部分销售资料．资料显示：11月2日开始，每天的销售量比前一天多t台(t为常数)，期间某天由于商家提高了家电M的价格，从当天起，每天的销售量比前一天少2台.11月份前2天共售出8台，11月5日的销售量为18台．

(1)若商家在11月1日至15日之间未提价，试求这15天家电M的总销售量．

(2)若11月1日至15日的总销售量为414台，试求11月份的哪一天，该商场售出家电M的台数最多？并求这一天售出的台数．

已知点A(－1,0)，B(1,0)，C(0,1)，直线y＝ax＋b(a>0)将△ABC分割为面积相等的两部分，则b的取值范围是(　　)

A．(0,1)                                B.

C.                           D.


设a∈R，则“a＝1”是“直线l1：ax＋2y－1＝0与直线l2：x＋(a＋1)y＋4＝0平行”的(　　)

A．充分不必要条件                       B．必要不充分条件

C．充分必要条件                         D．既不充分也不必要条件

平面直角坐标系中，过原点O的直线l与曲线y＝ex－1交于不同的A，B两点，分别过点A，B作y轴的平行线，与曲线y＝ln x交于点C，D，则直线CD的斜率是________．

如右图所示，圆O1和圆O2的半径长都等于1，|O1O2|＝4.过动点P分别作圆O1，圆O2的切线PM，PN(M，N为切点)，使得|PM|＝|PN|.试建立平面直角坐标系，并求动点P的轨迹方程．

已知F1，F2分别是双曲线x2－＝1的左、右焦点，A是双曲线上在第一象限内的点，若|AF2|＝2且∠F1AF2＝45°.延长AF2交双曲线右支于点B，则△F1AB的面积等于________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网