题目内容
4.将函数y=sin(2x-$\frac{π}{3}$)的图象先向左平移$\frac{π}{3}$个单位,再将图象上各点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),那么所得图象的解析式为y=sin(4x+$\frac{π}{3}$).分析 先求函数y=sin(2x-$\frac{π}{3}$)的图象先向左平移$\frac{π}{3}$,图象的函数表达式,再求图象上所有的点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),则所得到的图象对应的函数解析式.
解答 解:将函数y=sin(2x-$\frac{π}{3}$)的图象先向左平移$\frac{π}{3}$,
得到函数y=sin[2(x+$\frac{π}{3}$)-$\frac{π}{3}$]=sin(2x+$\frac{π}{3}$)的图象,
将所得图象上所有的点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),
则所得到的图象对应的函数解析式为:y=sin(4x+$\frac{π}{3}$ )
故答案为:sin(4x+$\frac{π}{3}$ ).
点评 本题考查函数y=Asin(ωx+φ)的图象变换,考查分析问题解决问题的能力,是基础题.

练习册系列答案
相关题目
14.直线y=2x-3在y轴上的截距是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
14.过抛物线y2=2px(p>0)的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则$\frac{{|{PQ}|}}{{|{MN}|}}$的最大值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
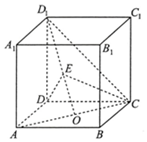 (理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.
(理科)如图,在正方体ABCD-A1B1C1D1,O是AC的中点,E是线段D1O上一点,且$\frac{{D}_{1}E}{EO}$=λ.