题目内容
13.已知函数f(x)=alnx+$\frac{1}{x}$(a≠0).(1)求函数f(x)的单调区间;
(2)若{x|f(x)<0}⊆(0,e${\;}^{-\frac{1}{2}}$),求实数a的取值范围.
分析 (1)先求出函数的导数,通过讨论a的范围,从而求出函数的单调区间.
(2)讨论a的取值范围,求出不等式f(x)<0的解集,结合集合的关系进行求解即可.
解答 解:(1)函数的定义域为(0,+∞),
则函数的导数f′(x)=$\frac{a}{x}$-$\frac{1}{{x}^{2}}$=$\frac{ax-1}{{x}^{2}}$,(x>0),
当a<0时,则f′(x)<0,f(x)在(0,+∞)递减;
若a>0时:令f′(x)>0,解得:x>$\frac{1}{a}$,
令f′(x)<0,解得:0<x<$\frac{1}{a}$,
∴f(x)在(0,$\frac{1}{a}$)递减,在($\frac{1}{a}$,+∞)递增.
(2)若a<0,则函数在(0,+∞)递减,且当x→0时,f(x)→+∞,则不满足条件{x|f(x)<0}⊆(0,e${\;}^{-\frac{1}{2}}$),
若a>0,在f(x)在(0,$\frac{1}{a}$)递减,在($\frac{1}{a}$,+∞)递增.
则当x=$\frac{1}{a}$时,函数取得极小值,同时也是最小值,此时f($\frac{1}{a}$)=aln$\frac{1}{a}$+a=-alna+a=-a(lna-1)=a(1-lna),
①若f($\frac{1}{a}$)=a(1-lna)>0,即0<a<e时,{x|f(x)<0}=∅⊆(0,e${\;}^{-\frac{1}{2}}$),满足条件,
②若f($\frac{1}{a}$)=a(1-lna)=0,即a=e时,{x|f(x)<0}={$\frac{1}{e}$}⊆(0,e${\;}^{-\frac{1}{2}}$),满足条件,
③若f($\frac{1}{a}$)=a(1-lna)<0,即a>e时,0<$\frac{1}{a}$<1,
∵f(1)=1>0,∴f(x)在($\frac{1}{a}$,+∞)递增.
∴当x≥1时,f(x)>0,
∵函数f(x)的定义域为(0,+∞),∴{x|f(x)≤0}⊆(0,e${\;}^{-\frac{1}{2}}$),成立,
综上a>0.
点评 本题主要考查函数单调性和单调区间的判断,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.要注意对参数进行分类讨论.

 阅读快车系列答案
阅读快车系列答案| A. | 6 | B. | $\sqrt{3}$(1+$\sqrt{2}$+$\sqrt{3}$) | C. | 3+3$\sqrt{2}$ | D. | 3+3$\sqrt{3}$ |
| A. | a+3 | B. | -a+5 | C. | a-5 | D. | -a-3 |
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
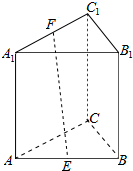 如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.
如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.