题目内容
过抛物线y2=4x的焦点F的直线交该抛物线与A、B两点,若|BF|=
,|AF|= .
| 3 |
| 2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线方程求得p和F点的坐标,根据|BF|求得B点的横坐标,代入抛物线方程求得其纵坐标,进而得到直线AB的方程与抛物线方程联立消去y,利用韦达定理求得xA+xB,进而求得|AB|,最后利用|AB|-|BF|求得答案.
解答:
解:依题意2p=4,
∴p=2,F坐标为(1,0),
∵点B到准线的距离与|BF|相等,即为
,
∴xB=
-1=
,
∴yB=±
当点B在y轴上方时,yB=
∴直线AB的方程为
=
,即y=-2
x+2
,与抛物线方程联立得,
2x2-5x+2=0,
∴xA+xB=
,
∴|AB|=xA+xB+p=
+2=
∴|AF|=|AB|-|BF|=
-
=3
故答案为:3.
∴p=2,F坐标为(1,0),
∵点B到准线的距离与|BF|相等,即为
| 3 |
| 2 |
∴xB=
| 3 |
| 2 |
| 1 |
| 2 |
∴yB=±
| 2 |
当点B在y轴上方时,yB=
| 2 |
∴直线AB的方程为
| x-1 |
| y |
1-
| ||
|
| 2 |
| 2 |
2x2-5x+2=0,
∴xA+xB=
| 5 |
| 2 |
∴|AB|=xA+xB+p=
| 5 |
| 2 |
| 9 |
| 2 |
∴|AF|=|AB|-|BF|=
| 9 |
| 2 |
| 3 |
| 2 |
故答案为:3.
点评:本题主要考查了抛物线简单性质.活用圆锥曲线的定义是解决圆锥曲线最基本的方法.到焦点的距离,叫焦半径.到焦点的距离常转化到准线的距离求解.

练习册系列答案
相关题目
在△ABC中,边a,b,c所对的角分别为A,B,C,若a=
,b=
,B=60°,则A=( )
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、90° |

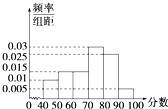 某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为
某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图形的信息,回答下列问题:估计这次考试的及格率(60分及以上为及格)为