题目内容
在区间[0，2]上随机取两个数x，y，则0≤xy≤2的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：先作出图象，由题意可设两个数为x，y，则有所有的基本事件满足
，所研究的事件满足0≤y≤
，再利用图形求概率．
|
| 2 |
| x |
解答：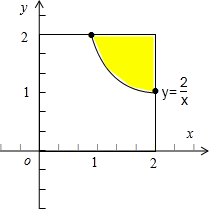
解：由题意可设两个数为x，y，则所有的基本事件满足
，所研究的事件满足0≤y≤
，如图．
总的区域是一个边长为2的正方形，它的面积是4，
满足0≤y≤
的区域的面积是4-
(2-
)dx=4-(2x-2lnx)
=4-[（4-2ln2）-（2-2ln1）]=2+2ln2，
则0≤xy≤2的概率为P=
=
，
故选：C．
解：由题意可设两个数为x，y，则所有的基本事件满足
|
| 2 |
| x |
总的区域是一个边长为2的正方形，它的面积是4，
满足0≤y≤
| 2 |
| x |
| ∫ | 2 1 |
| 2 |
| x |
| | | 2 1 |
则0≤xy≤2的概率为P=
| 2+2ln2 |
| 4 |
| 1+ln2 |
| 2 |
故选：C．
点评：本题考查几何概率模型，求解问题的关键是能将问题转化为几何概率模型求解，熟练掌握几何概率模型的特征利于本题的转化．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
x∈(0，＋∞)取最小值时x的值，列表如下：
(x＞0)在区间(0，2)上递减；函数f(x)＝
，x∈(0，＋∞)的最小值，并确定取得最小值时x的值，列表如下：
，x∈(0，＋∞)的部分性质，先列表如下：
(x＞0)在区间________上递增．当x＝________时，y最小＝________．
，x∈(0，＋∞)的最小值，并确定相应的x的值，列表如下：
，(x＞0)在区间(0，2)上递减，则在区间________上递增；
，(x＞0)的最小值为________；
，在区间(0，2)上单调递减．
，x∈(0，+∞)的最小值，并确定相应的x的值，列表如下：
（x＞0）在区间(0，2)上递减，则在________上递增；
（x＞0）在区间(0，2)上递减；
（x＜0）有最值吗？是最大值还是最小值？此时x为何值？