题目内容
(本小题满分12分)
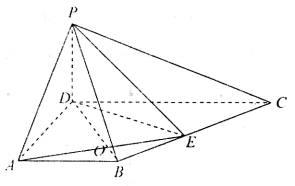
如图,ABCD为梯形,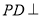 平面ABCD,AB//CD,
平面ABCD,AB//CD,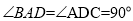
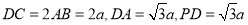 ,E为BC中点,连结AE,交BD于O.
,E为BC中点,连结AE,交BD于O.
(I)平面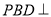 平面PAE
平面PAE
(II)求二面角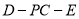 的大小(若非特殊角,求出其余弦即可)
的大小(若非特殊角,求出其余弦即可)
(1)见解析;(2)
【解析】
试题分析:(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2)作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
试题解析:(Ⅰ)连结


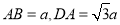 ,所以
,所以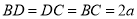
 为
为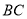 中点,所以,
中点,所以,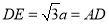
因为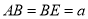 ,
,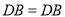
所以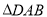 与
与 为全等三角形
为全等三角形
所以
所以 与
与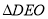 为全等三角形
为全等三角形
所以在 中,
中,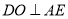 ,即
,即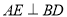 3分
3分
又因为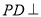 平面
平面 ,
, 平面
平面
所以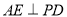 4分
4分
而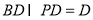
所以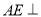 平面
平面 5分
5分
因为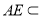 平面
平面
所以平面 平面
平面 6分
6分
(Ⅱ) 以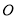 为原点,分别以
为原点,分别以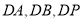 所在直线为
所在直线为 轴,建立空间直角坐标系如图
轴,建立空间直角坐标系如图

二面角 即二面角
即二面角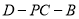
 平面
平面 ,平面
,平面 的法向量可设为
的法向量可设为
 7分
7分
设平面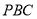 的法向量为
的法向量为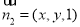
所以 ,而
,而

即: ,可求得
,可求得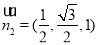 10分
10分

所以两平面 与平面
与平面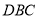 所成的角的余弦值
所成的角的余弦值
为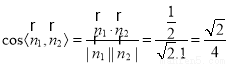 12分
12分
考点:空间几何的位置关系.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 门课程中各选修
门课程中各选修 门,则甲乙所选的课程中恰有
门,则甲乙所选的课程中恰有 门相同的选法有 种.
门相同的选法有 种.  的展开式中x的系数为
的展开式中x的系数为 B.20 C.
B.20 C.  D.40
D.40 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 B.
B. 
 D.
D. 
 是纯虚数,则实数
是纯虚数,则实数 的值为
的值为 B.
B.  C.
C.  D.
D. 
 所围成的图形的面积是_________.
所围成的图形的面积是_________.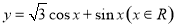 的图像向左平移个
的图像向左平移个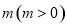 单位长度后,所得的图像关于
单位长度后,所得的图像关于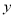 轴对称,则
轴对称,则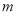 的最小值是
的最小值是 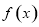 的定义域为
的定义域为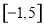 ,部分对应值如下表,
,部分对应值如下表,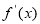 的图象如图所示.
的图象如图所示.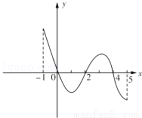
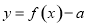 有
有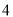 个零点,则实数
个零点,则实数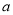 的取值范围为( )
的取值范围为( )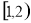 (B)
(B)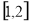 (C)
(C) 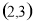 (D)
(D)