题目内容
2.i是虚数单位,复数z=${({\frac{3-i}{1+i}})^2}$,则复数z的共轭复数表示的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接利用复数代数形式的乘除运算化简求得z,进一步得到$\overline{z}$得答案.
解答 解:∵z=${({\frac{3-i}{1+i}})^2}$=$[\frac{(3-i)(1-i)}{(1+i)(1-i)}]^{2}=(\frac{2-4i}{2})^{2}=(1-2i)^{2}=-3-4i$,
∴$\overline{z}=-3+4i$.
∴复数z的共轭复数表示的点的坐标为(-3,4),在第二象限.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设数列{an}的前n项和为Sn,对任意n∈N*,函数f(x)=x2-Sncosx+2an-n在定义域内有唯一的零点.若不等式$\frac{λ}{n}$≥$\frac{n+1}{{a}_{n}+1}$对任意n∈N*恒成立,则实数λ的最小值是( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
10.若曲线y=$\sqrt{4-{x^2}}$+1与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
| A. | $({\frac{5}{12},\frac{3}{4}}]$ | B. | $[{\frac{5}{12},+∞})$ | C. | $({0,\frac{5}{12}}]$ | D. | $({\frac{1}{3},\frac{1}{4}}]$ |
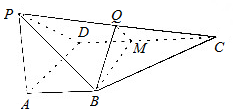 四棱锥P-ABCD中,PA⊥底面ABCDD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°,M是CD上的点,Q点是PC上的点,平面BMQ∥平面PAD.
四棱锥P-ABCD中,PA⊥底面ABCDD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°,M是CD上的点,Q点是PC上的点,平面BMQ∥平面PAD.