题目内容
9.设双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)与抛物线y2=8x交于两点A,B,且|AB|=8,则该双曲线的焦点到其渐近线的距离为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{\sqrt{6}}{3}$ |
分析 运用双曲线和抛物线的对称性,可设A(m,4),B(m,-4),代入抛物线的方程可得m=2,求得A(2,4),代入双曲线的方程可得b=4,再由点到直线的距离公式可得所求值.
解答 解:由双曲线和抛物线关于x轴对称可得,
A,B关于x轴对称,
由|AB|=8,可设A(m,4),B(m,-4),
代入抛物线y2=8x,即有16=8m,解得m=2,
即有A(2,4),代入双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
可得2-$\frac{16}{{b}^{2}}$=1,解得b=4,
则双曲线的焦点(c,0)到其渐近线y=$\frac{b}{a}$x的距离为
d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b=4.
故选:C.
点评 本题考查双曲线的焦点到渐近线的距离,注意运用抛物线和双曲线的对称性,以及代入法,考查运算能力,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的斜率为2,过右焦点F作x轴的垂线交双曲线与A,B两点,△OAB(O为坐标原点)的面积为4$\sqrt{5}$,则F到一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
14.已知倾斜角为$\frac{π}{3}$的直线与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}+1}{2}$ |
1.若直线y=x-2过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的焦点,则此双曲线C的渐近线方程为( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=$±\sqrt{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±$\frac{\sqrt{5}}{5}$x |
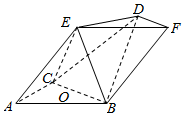 如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.