题目内容
已知二项式(
-
)n的展开式中,二项式系数的和为256,
(1)求n的值;
(2)求展开式中的二项式系数最大的项;
(3)求展开式中各项的系数和.
| 3 | x |
| 1 | |||
2
|
(1)求n的值;
(2)求展开式中的二项式系数最大的项;
(3)求展开式中各项的系数和.
考点:二项式系数的性质,二项式定理的应用
专题:二项式定理
分析:(1)依题意知(
-
)n展开式中的二项式系数的和为2n=256,由此求得n的值
(2)由展开式的通项公式为 Tr+1=
(-
)rx
,而展开式中的二项式系数最大的项为中间项,即第五项,
从而求得结果.
(3)令x=1得各项系数和.
| 3 | x |
| 1 | |||
2
|
(2)由展开式的通项公式为 Tr+1=
| C | r 8 |
| 1 |
| 2 |
| 8-2r |
| 3 |
从而求得结果.
(3)令x=1得各项系数和.
解答:
解:(1)依题意知(
-
)n展开式中的二项式系数的和为2n=256,
∴n=8.
(2)由(1)知,展开式的通项公式为 Tr+1=
(-
)rx
,
∵展开式中的二项式系数最大的项为中间项,即第五项,
∴T5=
(-
)4=
.
(3)令x=1得各项系数和为(
)8=
.
| 3 | x |
| 1 | |||
2
|
∴n=8.
(2)由(1)知,展开式的通项公式为 Tr+1=
| C | r 8 |
| 1 |
| 2 |
| 8-2r |
| 3 |
∵展开式中的二项式系数最大的项为中间项,即第五项,
∴T5=
| C | 4 8 |
| 1 |
| 2 |
| 35 |
| 8 |
(3)令x=1得各项系数和为(
| 1 |
| 2 |
| 1 |
| 256 |
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
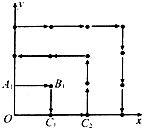 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么:
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点Al(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么: