题目内容
(本题满分16分)
设函数 .
.
(1)若 =1时,函数
=1时,函数 取最小值,求实数
取最小值,求实数 的值;
的值;
(2)若函数 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;
(3)若 ,证明对任意正整数
,证明对任意正整数 ,不等式
,不等式 都成立.
都成立.
(1)- 4.(2) (3)详见解析
(3)详见解析
【解析】
试题分析:(1)利用导数求开区间函数最值,先从导函数出发,探求极值点即为最值点,最后需列表验证:由 得
得 (2)函数
(2)函数 在定义域上是单调函数,即导函数不变号,
在定义域上是单调函数,即导函数不变号, ≥0或
≥0或 ≤0在( - 1,+ ∞)上恒成立. 即2x2 +2x+b≥0在( - 1,+ ∞)上恒成立或2x2 +2x+b≤0在( - 1,+ ∞)上恒成立,利用变量分离及函数最值可得:实数b的取值范围是
≤0在( - 1,+ ∞)上恒成立. 即2x2 +2x+b≥0在( - 1,+ ∞)上恒成立或2x2 +2x+b≤0在( - 1,+ ∞)上恒成立,利用变量分离及函数最值可得:实数b的取值范围是 .(3)证明和项不等式,关键分析出和项与通项关系:
.(3)证明和项不等式,关键分析出和项与通项关系: 即证当
即证当 时,有f(x) <x3.这可利用导数给予证明
时,有f(x) <x3.这可利用导数给予证明
试题解析:(1)由x + 1>0得x> – 1∴f(x)的定义域为( - 1,+ ∞),
对x∈ ( - 1,+ ∞),都有f(x)≥f(1),∴f(1)是函数f(x)的最小值,故有f/ (1) = 0,
 解得b= - 4. 经检验,列表(略),合题意;
解得b= - 4. 经检验,列表(略),合题意;
(2)∵ 又函数
又函数 在定义域上是单调函数,
在定义域上是单调函数,
∴ ≥0或
≥0或 ≤0在( - 1,+ ∞)上恒成立.
≤0在( - 1,+ ∞)上恒成立.
若 ≥0,∵x + 1>0,∴2x2 +2x+b≥0在( - 1,+ ∞)上恒成立,
≥0,∵x + 1>0,∴2x2 +2x+b≥0在( - 1,+ ∞)上恒成立,
即b≥-2x2 -2x =  恒成立,由此得b≥
恒成立,由此得b≥ ;
;
若 ≤0, ∵x + 1>0, ∴2x2 +2x+b≤0,即b≤- (2x2+2x)恒成立,
≤0, ∵x + 1>0, ∴2x2 +2x+b≤0,即b≤- (2x2+2x)恒成立,
因-(2x2+2x) 在( - 1,+ ∞)上没有最小值,∴不存在实数b使f(x) ≤0恒成立.
综上所述,实数b的取值范围是 .
.
(3)当b= - 1时,函数f(x) = x2 - ln(x+1),令函数h(x)=f(x) – x3 = x2 – ln(x+1) – x3,
则h/(x) = - 3x2 +2x -  ,
,
∴当 时,h/(x)<0所以函数h(x)在
时,h/(x)<0所以函数h(x)在 上是单调递减.
上是单调递减.
又h(0)=0,∴当 时,恒有h(x) <h(0)=0,即x2 – ln(x+1) <x3恒成立.
时,恒有h(x) <h(0)=0,即x2 – ln(x+1) <x3恒成立.
故当 时,有f(x) <x3..
时,有f(x) <x3..
∵ 取
取 则有
则有
∴ ,故结论成立。
,故结论成立。
考点:利用导数研究函数性质

 同步奥数系列答案
同步奥数系列答案 ,则
,则 的大小关系是( )
的大小关系是( ) (B)
(B) (C)
(C) (D)
(D)
 满足约束条件
满足约束条件 若
若 的最小值为
的最小值为 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
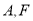 分别是椭圆
分别是椭圆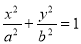
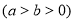 的上顶点和右焦点,直线
的上顶点和右焦点,直线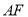 与椭圆交于另一点
与椭圆交于另一点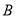 ,过中心
,过中心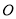 作直线
作直线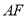 的平行线交椭圆于
的平行线交椭圆于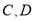 两点,若
两点,若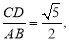 则椭圆的离心率为 .
则椭圆的离心率为 .
 中,各项都是正数,且
中,各项都是正数,且 成等差数列,则
成等差数列,则 等于 .
等于 . 则xy的取值范围是 .
则xy的取值范围是 .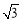 ,a+b=(
,a+b=(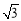 ,1),则向量a+b与向量a-b的夹角是 .
,1),则向量a+b与向量a-b的夹角是 . 的解集是 .
的解集是 .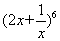 展开式中的常数项为 _________.
展开式中的常数项为 _________.