题目内容
15.给定矩阵A=$[\begin{array}{l}{1}&{2}\\{2}&{3}\end{array}]$,B=$[\begin{array}{l}{-\frac{3}{2}}&{2}\\{1}&{-1}\end{array}]$,设椭圆$\frac{{x}^{2}}{4}$+y2=1在矩阵AB对应的变换下得到曲线F,求F的面积.分析 求出AB,可得椭圆$\frac{{x}^{2}}{4}$+y2=1在矩阵AB对应的变换下得到曲线F,即可求F的面积.
解答 解:由已知得$AB=[\begin{array}{l}1\\ 2\end{array}\right.\;\;\;\left.\begin{array}{l}2\\ 3\end{array}][\begin{array}{l}-\frac{3}{2}\;\;\;\;2\\ \;\;1\;\;\;\;\;-1\end{array}]=[\begin{array}{l}\frac{1}{2}\;\;\;\;0\\ \;0\;\;\;\;1\end{array}]$,
设P(x0,y0)为椭圆上任意一点,点M在矩阵AB对应的变换下变为点$P'({x_0}^′,{y_0}^′)$,
则有$[\begin{array}{l}\frac{1}{2}\;\;\;\;0\\ \;0\;\;\;\;1\end{array}][\begin{array}{l}{x_0}\\{y_0}\end{array}]=[\begin{array}{l}{x_0}^′\\{y_0}^′\end{array}]$,即$\left\{\begin{array}{l}\frac{1}{2}{x_0}={x_0}^′\\{y_0}={y_0}^′\end{array}\right.$,所以$\left\{\begin{array}{l}{x_0}=2{x_0}^′\\{y_0}={y_0}^′\end{array}\right.$,
又点P在椭圆上,故$\frac{{{x_0}^2}}{4}+{y_0}^2=1$,从而${({x_0}^′)^2}+{({y_0}^′)^2}=1$,
故曲线F的方程为x2+y2=1,其面积为π.
点评 本题考查矩阵与变换,考查圆的方程,属于基础题.

| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
| A. | 667 | B. | 668 | C. | 669 | D. | 673 |
| A. | $\frac{1}{5}$ | B. | 5 | C. | $-\frac{1}{5}$ | D. | -5 |
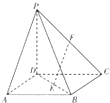 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.