题目内容
2.y=$\frac{(x-2)\sqrt{1-{x}^{2}}}{\sqrt{{x}^{2}-4x+4}}$值域为[-1,0].分析 求出函数的定义域,将函数进行化简,然后进行求解即可.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{1-{x}^{2}≥0}\\{{x}^{2}-4x+4>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-1≤x≤1}\\{(x-2)^{2}>0}\end{array}\right.$,得$\left\{\begin{array}{l}{-1≤x≤1}\\{x≠2}\end{array}\right.$,
则-1≤x≤1,即函数的定义域为[-1,1],
此时y=$\frac{(x-2)\sqrt{1-{x}^{2}}}{\sqrt{{x}^{2}-4x+4}}$=$\frac{(x-2)\sqrt{1-{x}^{2}}}{|x-2|}$=$\frac{(x-2)\sqrt{1-{x}^{2}}}{-(x-2)}$=-$\sqrt{1-{x}^{2}}$,
∵0≤$\sqrt{1-{x}^{2}}$≤1,
∴-1≤-$\sqrt{1-{x}^{2}}$≤0,
即函数的值域为[-1,0],
故答案为:[-1,0].
点评 本题主要考查函数值域的求解,本题先求出函数的定义域,将函数进行化简是解决本题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
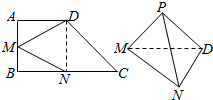 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 圆的方程是(x-2)2+(y-1)2=1,P是直线x+y+1=0上任意一点,经过P作圆的切线,求切线长的最小值以及相应P点坐标.
圆的方程是(x-2)2+(y-1)2=1,P是直线x+y+1=0上任意一点,经过P作圆的切线,求切线长的最小值以及相应P点坐标.