题目内容
4.△ABC中,角A,B,C所对边分别为a,b,c,△ABC的面积为S,若4$\sqrt{3}$S=(a+b)2-c2,则角C的大小为$\frac{π}{3}$.分析 由题意和三角形的面积公式以及余弦定理可得$\sqrt{3}$sinC=cosC+1,再由和差角的三角函数公式和三角形内角的范围可得.
解答 解:∵△ABC中4$\sqrt{3}$S=(a+b)2-c2,
∴4$\sqrt{3}$×$\frac{1}{2}$absinC=a2+b2-c2+2ab,
∴由余弦定理可得2$\sqrt{3}$absinC=2abcosC+2ab,
约掉2ab可得$\sqrt{3}$sinC=cosC+1,即$\sqrt{3}$sinC-cosC=1,
∴2sin(C-$\frac{π}{6}$)=1,故sin(C-$\frac{π}{6}$)=$\frac{1}{2}$,
∴C-$\frac{π}{6}$=$\frac{π}{6}$或C-$\frac{π}{6}$=$\frac{5π}{6}$,解得C=$\frac{π}{3}$或C=π(舍去)
故答案为:$\frac{π}{3}$.
点评 本题考查正余弦定理解三角形以及三角形的面积公式,涉及和差角的三角函数公式,属中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.已知tanα=2,则tan(α-$\frac{π}{6}$)=( )
| A. | 8-5$\sqrt{3}$ | B. | 6-5$\sqrt{3}$ | C. | 5$\sqrt{3}$-8 | D. | 5$\sqrt{3}$-6 |
19.若α是第二象限角,且sinα=$\frac{3}{5}$,则cosα=( )
| A. | $\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{4}{5}$ | D. | $\frac{3}{5}$ |
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.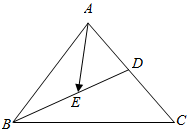 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.