题目内容
16.若随机变量X~N(u,σ2)(σ>0),则有如下结论( )P(u-σ<X≤u+σ)=0.6826,
P(u-2σ<X≤u+2σ)=0.9544
P(u-3σ<X≤u+3σ)=0.9974,
一班有60名同学,一次数学考试的成绩服从正态分布,平均分110,方差为100,理论上说在120分到130分之间的人数约为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 正态总体的取值关于x=110对称,利用P(100<x<120)=0.6826,P(90<x<130)=0.9544,得即可到要求的结果.
解答 解:∵数学成绩近似地服从正态分布N(110,102),
∴P(100<x<120)=0.6826,P(90<x<130)=0.9544,
根据正态曲线的对称性知:
位于120分到130分的概率为$\frac{1}{2}(0.9544-0.6826)$=0.1359
∴理论上说在120分到130分的人数0.1359×60≈8.
故选:C.
点评 一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似的服从正态分布,正态分布在概率和统计中具有重要地位且满足3σ原则.

练习册系列答案
相关题目
11.已知全集U=R,A={x|x2-3x-4>0},B={x|-2≤x≤2},则如图所示的阴影部分所表示的集合为( )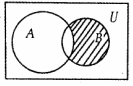

| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |
8.已知全集U={0,1,2,3,4},集合M={1,2,3},N={0,3,4},则(∁UM)∩N( )
| A. | {0,4} | B. | {3,4} | C. | {1,2} | D. | ∅ |
16.若sinθ+coθ=$\frac{2}{3}$,则sinθ-cosθ=( )
| A. | $\frac{\sqrt{14}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | ±$\frac{\sqrt{14}}{3}$ | D. | ±$\frac{\sqrt{6}}{3}$ |