Question

已知实数x，y满足约束条件

x-y+6≥0 x+y≥0 x≤3

则z=

9x

3-y

的最小值为 （　　）

• A、27
• B、

  1

  27

• C、3
• D、

  1

  3

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：化简目标函数为z=3^2x+y，令m=2x+y，利用数形结合得到m的最小值即可得到结论．

解答： 解：作出不等式组对应的平面区域如图：（阴影部分）．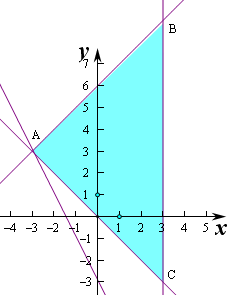
z=

9x

3-y

=3^2x+y，令m=2x+y，得y=-2x+m，
平移直线y=-2x+m，
由图象可知当直线y=-2x+m经过点A（0，-1）时，
直线y=-2x+m的截距最小，
此时m最小．
由

x-y+6=0 x+y=0

，

x=-3 y=3

，即A（-3，3）代入目标函数m=2x+y，
得m=-6+3=-3．
即z=3^m的最小值为3-3=

1

27

．
故选：B．

点评：本题主要考查线性规划的应用，结合目标函数的几何意义，利用数形结合的数学思想是解决此类问题的基本方法．