题目内容
下列函数在定义域上既是奇函数,又是单调递增函数的是( )
| A、y=x|x| | ||||||
| B、y=ex+e-x | ||||||
C、y=
| ||||||
D、y=x
|
考点:幂函数的单调性、奇偶性及其应用,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:A.运用函数的奇偶性定义和单调性,注意去绝对值,即可判断A;
B.由奇偶性定义判断为偶函数,故B不正确;
C.由奇偶性定义判断为奇函数,但不为增函数,可举反例;
D.由定义域不关于原点对称,即可判断函数不具有奇偶性.
B.由奇偶性定义判断为偶函数,故B不正确;
C.由奇偶性定义判断为奇函数,但不为增函数,可举反例;
D.由定义域不关于原点对称,即可判断函数不具有奇偶性.
解答:
解:A.f(x)=x|x|的定义域为R,f(-x)=-x|-x|=-f(x)∴函数在定义域上是奇函数,
当x≥0时,y=x2为增函数,当x<0时,y=-x2为增函数,且函数为连续函数,∴此函数为单调递增函数.
故A正确;
B.f(x)=ex+e-x的定义域为R,f(-x)=e-x+ex即f(x)=f(-x),∴此函数是偶函数不是奇函数,故B错误;
C.当x=0时,f(0)=0,f(-x)=-f(x),∵x>0,f(x)=x-1;x<0时,f(x)=x+1.若x<0则-x>0,f(-x)=-x-1=-f(x),
若x>0则-x<0,f(-x)=-x+1=-f(x),故对x∈R,f(-x)=-f(x),即f(x)奇函数,可举x1=-1,x2=
,f(x1)=0,f(x2)=-
,即x1<x2,f(x1)>f(x2),故C项错误;
D.y=x
=
的定义域为{x|x≥0}不关于原点对称,∴此函数没有奇偶性,故D项错误.
故选A.
当x≥0时,y=x2为增函数,当x<0时,y=-x2为增函数,且函数为连续函数,∴此函数为单调递增函数.
故A正确;
B.f(x)=ex+e-x的定义域为R,f(-x)=e-x+ex即f(x)=f(-x),∴此函数是偶函数不是奇函数,故B错误;
C.当x=0时,f(0)=0,f(-x)=-f(x),∵x>0,f(x)=x-1;x<0时,f(x)=x+1.若x<0则-x>0,f(-x)=-x-1=-f(x),
若x>0则-x<0,f(-x)=-x+1=-f(x),故对x∈R,f(-x)=-f(x),即f(x)奇函数,可举x1=-1,x2=
| 1 |
| 2 |
| 1 |
| 2 |
D.y=x
| 5 |
| 2 |
| 2 | x5 |
故选A.
点评:本题主要考查函数的性质:奇偶性、单调性,注意函数的定义域关于原点对称是函数具有奇偶性的必要条件,函数的单调性的判断,必须注意定义中的任意自变量.

练习册系列答案
相关题目
已知数列{an}的前n项和为Sn=n2-5n+2,则数列{|an|}的前10项和为( )
| A、56 | B、58 | C、62 | D、60 |
在△ABC中的内角A,B,C所对的边分别为a,b,c,若∠B=60°,a,b,c成等比数列,则△ABC的形状为( )
| A、直角三角形 | B、等腰三角形 |
| C、等边三角形 | D、不确定 |
若f(x)是R上的可导函数,且f(x)+xf′(x)>0则下列结论正确的是( )
| A、2014f(2014)>2015f(2015) |
| B、2014f(2015)>2015f(2014) |
| C、2014f(2014)<2015f(2015) |
| D、2014f(2015)<2015f(2014) |
已知命题p:?x∈R,ax>0(a>0且a≠1),则( )
| A、¬p:?x∈R,ax≤0 |
| B、¬p:?x∈R,ax>0 |
| C、¬p:?x0∈R,a x0>0 |
| D、¬p:?x0∈R,a x0≤0 |
已知实数x,y满足约束条件
则z=
的最小值为 ( )
|
| 9x |
| 3-y |
| A、27 | ||
B、
| ||
| C、3 | ||
D、
|
如图是导函数y=f′(x)的图象,那么函数y=f(x)在下面哪个区间是减函数( )
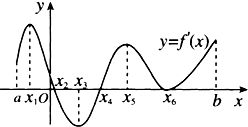

| A、(x1,x3) |
| B、(x2,x4) |
| C、(x4,x6) |
| D、(x5,x6) |
执行所示的程序框图,如果输入N=5,则输出的数等于( )
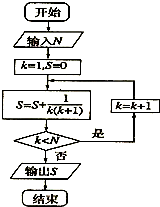

A、
| ||
B、
| ||
C、
| ||
D、
|