题目内容
4.若函数f(x)=loga(x3-2x)(a>0且a≠1)在区间(-$\sqrt{2}$,-1)内恒有f(x)>0,则f(x)的单调递减区间为( )| A. | (-∞,-$\frac{{\sqrt{6}}}{3}$),($\frac{{\sqrt{6}}}{3}$,+∞) | B. | (-$\sqrt{2}$,-$\frac{{\sqrt{6}}}{3}$),($\sqrt{2}$,+∞) | C. | (-$\sqrt{2}$,-$\frac{{\sqrt{6}}}{3}$),($\frac{{\sqrt{6}}}{3}$,+∞) | D. | (-$\frac{{\sqrt{6}}}{3}$,$\frac{{\sqrt{6}}}{3}$) |
分析 求函数的定义域,利用换元法结合条件判断a的取值范围,利用复合函数和导数即可求出函数单调递减区间.
解答  解:设t=g(t)=x3-2x,
解:设t=g(t)=x3-2x,
由t=0得x(x2-2)=0,
则x=0,或x=$\sqrt{2}$或x=-$\sqrt{2}$,
由x3-2x>0得-$\sqrt{2}$<x<0或x>$\sqrt{2}$,
g′(t)=3x2-2,当-$\sqrt{2}$<x<-1时,g′(t)>0,此时函数g(t)为增函数,
则0<g(t)<1,
若a>1,则y=logat<0恒成立,则不满足条件f(x)>0,
若0<a<1,则y=logat>0恒成立,满足条件,即0<a<1,
要求函数f(x)的单调递减区间,即求函数t=g(t)=x3-2x的递增区间,
由g′(t)=3x2-2>0得x<-$\frac{{\sqrt{6}}}{3}$或x>$\frac{{\sqrt{6}}}{3}$,
∵-$\sqrt{2}$<x<0或x>$\sqrt{2}$,
∴-$\sqrt{2}$<x<-$\frac{{\sqrt{6}}}{3}$或x>$\sqrt{2}$,
即函数f(x)的单调递减区间为(-$\sqrt{2}$,-$\frac{{\sqrt{6}}}{3}$),($\sqrt{2}$,+∞),
故选:B
点评 本题主要考查函数单调区间的求解决,利用换元法以及导数法是解决本题的关键.考查学生的运算和推理能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
16.已知a>0且 a≠1,函数f(x)=$\frac{3{a}^{x}+1}{{a}^{x}+1}$+3loga$\frac{1+x}{1-x}$(-$\frac{1}{2}$≤x≤$\frac{1}{2}$),设函数f(x)的最大值是A,最小值是B,则( )
| A. | A-B=4 | B. | A+B=4 | C. | A-B=6 | D. | A+B=6 |
13.已知集合A={2,3,4},B={2,4,6},则A∩B=( )
| A. | {2} | B. | {2,4} | C. | {2,4,6} | D. | {2,3,4,6} |
15.若执行如图所示的程序框图后,输出的结果是-29,则判断框中的整数k的值是( )
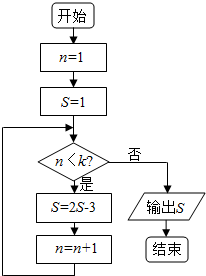

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |