题目内容
13.已知三点A(1,2),B(-6,x),C(-1,4)共线,求实数x的值.分析 因为A,B,C三点共线,所以,kAB=kAC,即,$\frac{x-2}{-6-1}$=$\frac{4-2}{-1-1}$,解得x=9.
解答 解:方法一:
因为A,B,C三点共线,
所以,kAB=kAC,
即,$\frac{x-2}{-6-1}$=$\frac{4-2}{-1-1}$,
解得x=9,故实数x的为为9.
方法二:
设直线AC的方程为y=kx+b,
代入A,C的坐标,解得k=-1,b=3,
所以,当x=-6时,y=9,
即B的纵坐标为9.
点评 本题主要考查了直线斜率的应用,将三点共线问题转化为两点连线斜率相等问题,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积为( )
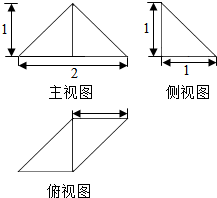

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
1.设集合A={x|x≥3},B={x|x≤3},则A∩B=( )
| A. | ∅ | B. | R | C. | {x||x≤3} | D. | {3} |