题目内容
已知△ABC是边长为2的正三角形，B为线段EF的中点，且EF=3，则
•
+
•
的取值范围是（ ）
| AB |
| AE |
| AC |
| AF |
| A、[0，3] |
| B、[3，6] |
| C、[6，9] |
| D、[3，9] |
考点：平面向量数量积的含义与物理意义
专题：平面向量及应用
分析：画出图形，把
•
+
•
的运算化为已知的
、
与
、
的数量积的运算，从而求得取值范围．
| AB |
| AE |
| AC |
| AF |
| AB |
| BC |
| BE |
| BF |
解答：
解：∵△ABC是边长为2的正三角形，B为线段EF的中点，且EF=3，如图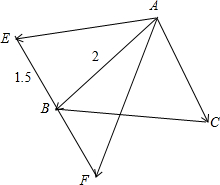
；
设∠ABF=θ，则θ∈[0，π]；
∴
•
+
•
=
•（
+
）+（
+
）•（
+
）
=
2+
•
+
2+
•
+
•
+
•
=2
2+（
•
+
•
）+
•
+
•
=2×22+0+2×2×cos
+2×
×cosθ
=6+3cosθ；
∵-1≤cosθ≤1，∴3≤6+cosθ≤9，
∴
•
+
•
的取值范围是[3，9]；
故选：D．
；设∠ABF=θ，则θ∈[0，π]；
∴
| AB |
| AE |
| AC |
| AF |
| AB |
| AB |
| BE |
| AB |
| BC |
| AB |
| BF |
=
| AB |
| AB |
| BE |
| AB |
| AB |
| BF |
| BC |
| AB |
| BC |
| BF |
=2
| AB |
| AB |
| BE |
| AB |
| BF |
| BC |
| AB |
| BC |
| BF |
=2×22+0+2×2×cos
| 2π |
| 3 |
| 3 |
| 2 |
=6+3cosθ；
∵-1≤cosθ≤1，∴3≤6+cosθ≤9，
∴
| AB |
| AE |
| AC |
| AF |
故选：D．
点评：本题考查了平面向量的加减运算以及数量积的综合运算，是易错题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
某几何体的三视图如图所示，则此几何体的体积是（ ）
A、
| ||
| B、6π | ||
C、
| ||
D、
|
如图，半径为R的半圆内的阴影部分以直径AB所在直线为轴，旋转一周得到一几何体，求该几何体的体积，（其中∠BAC=30°）
如图，设D是边长为l的正方形区域，E是D内函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
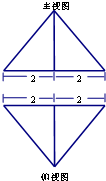三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形，其中底边长为4，腰长为3，则该三棱锥左视图的面积为（ ）