题目内容
10．点（a，b）在直线x+2y-1=0上，则a2+b2的最小值为$\frac{1}{5}$．分析 点（a，b）在直线x+2y-1=0上，因此$\sqrt{{a}^{2}+{b}^{2}}$的最小值为原点到直线的距离，即可得出．
解答 解：∵点（a，b）在直线x+2y-1=0上，
∴$\sqrt{{a}^{2}+{b}^{2}}$的最小值为原点到直线的距离d=$\frac{1}{\sqrt{5}}$，
则a2+b2的最小值为$\frac{1}{5}$．
故答案为：$\frac{1}{5}$．
点评 本题考查了点到直线距离公式，考查了转化能力与计算能力，属于中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
1．已知角α的终边与单位圆交于点P（-$\frac{3}{5}$，$\frac{4}{5}$），则cosα的值为（ ）
| A． | $\frac{3}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | -$\frac{4}{5}$ |
18．已知a，b∈R，则“0≤a≤1且0≤b≤1”是“0≤ab≤1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
5．抛掷两颗质地均匀的骰子，则点数之和为6的概率等于（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{5}{36}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{12}$ |
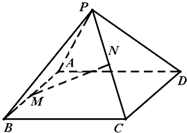已知正四棱锥P-ABCD如图．