题目内容
5.已知数列{an}为等差数列,公差d≠0{an}的部分项组成的数列ak1,ak2,…,akn恰为等比数列,其中k1=1,k2=5,k3=17,则kn=2•3n-1-1.分析 运用等差(比)数列的定义分别求得${a}_{{k}_{n}}$,然后列方程求得kn.
解答 解:设{an}的首项为a1,
∵${a}_{{k}_{1}}$,${a}_{{k}_{2}}$,${a}_{{k}_{3}}$成等比数列,
∴(a1+4d)2=a1(a1+16d).
得a1=2d,q=$\frac{{a}_{{k}_{2}}}{{a}_{{k}_{1}}}$=3.
∵${a}_{{k}_{n}}$=a1+(kn-1)d,又${a}_{{k}_{n}}$=a1•3n-1,
∴kn=2•3n-1-1.
故答案为:2•3n-1-1.
点评 运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:akn是等差数列中的第kn项,而是等比数列中的第n项,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在△ABC中,内角A,B,C所对边长分别为a,b,c,若a=$\sqrt{3}$,c-b=1,cos A=$\frac{2}{3}$,则△ABC的面积是$\frac{\sqrt{5}}{2}$.
20.已知△ABC的三边分别为a=7、b=5、c=3,则△ABC的最大内角等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
10.已知某车间加工零件的个数x与所花时间y(单位:h)之间的回归直线方程为$\widehat{y}$=0.01x+0.5,则加工600个零件大约需要( )
| A. | 6.5 h | B. | 5.5 h | C. | 3.5 h | D. | 0.5 h |
17.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤0)}\\{lo{{g}_{\frac{1}{2}}}{|x-1|}(x>0且x≠1)}\end{array}\right.$,若互不相等的实数a,b,c满足f(a)=f(b)=f(c),则a+b+c的取值范围是( )
| A. | (-∞,2] | B. | (-∞,1] | C. | (1,2) | D. | (2,+∞) |
14.如图所示,表示阴影部分的二元一次不等式组是( )
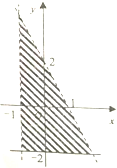

| A. | $\left\{\begin{array}{l}{x+1>0}\\{2x+y<2}\\{y≥-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y≤2}\\{y>-2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+1≥0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{2x+y<2}\\{y>-2}\end{array}\right.$ |