题目内容
若函数f(x)=sin3xcosx+cos3xsinx+
sin2x.
(1)求函数f(x)的单调递减区间;
(2)已知△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,若
•
=S,求f(A)的取值范围.
| 3 |
(1)求函数f(x)的单调递减区间;
(2)已知△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,若
| ||
| 2 |
| AB |
| BC |
考点:解三角形,三角函数中的恒等变换应用,复合三角函数的单调性
专题:计算题
分析:{1}利用平方关系式以及二倍角公式、两角和的正弦函数化简函数为一个角的一个三角函数的形式,通过正弦函数的单调性求出函数的单调减区间.
(2)利用三角形的面积与已知的表达式,求出B的值,推出A的范围,然后求出f(A)的范围.
(2)利用三角形的面积与已知的表达式,求出B的值,推出A的范围,然后求出f(A)的范围.
解答:
解:(1)函数f(x)=sin3xcosx+cos3xsinx+
sin2x
=sin xcosx+
sin2x
=
sin2x+
-
=sin(2x-
)+
.
由2kπ+
≤2x-
≤2kπ+
,k∈Z,
解得:x∈[kπ+
,kπ+
],k∈Z.
即函数的单调增区间为:[kπ+
,kπ+
],k∈Z.
(2)△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,
•
=S,
所以
|•|
|cos(π-B)=
|•|
|sinB,
tanB=-
,B=
.
0<A<
,
f(A)=sin(2A-
)+
,所以2A-
∈(-
,
),
sin(2A-
)∈(-
,
),sin(2A-
)+
∈(-
,
),
所以f(A)的范围:(-
,
).
| 3 |
=sin xcosx+
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 3 |
| ||
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得:x∈[kπ+
| 5π |
| 12 |
| 11π |
| 12 |
即函数的单调增区间为:[kπ+
| 5π |
| 12 |
| 11π |
| 12 |
(2)△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,
| ||
| 2 |
| AB |
| BC |
所以
| ||
| 2 |
| |AB |
| BC |
| 1 |
| 2 |
| |AB |
| BC |
tanB=-
| 3 |
| 2π |
| 3 |
0<A<
| π |
| 3 |
f(A)=sin(2A-
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
sin(2A-
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
所以f(A)的范围:(-
| 3 |
| 3 |
点评:本题考查二倍角公式与两角差的正弦函数的应用,函数的单调区间的求法,向量的数量积与三角形的面积公式的应用,三角函数的值域的求法,考查计算能力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
如果a
=b(a>0,且a≠1),则( )
| 1 |
| 2 |
A、log
| ||||
B、log
| ||||
C、log
| ||||
D、log
|
已知某个几何体的三视图如右,那么可得这个几何体的体积是( )
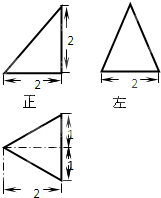

A、
| ||
B、
| ||
C、
| ||
D、
|
已知α,β都是锐角,cos2α=-
,cos(α+β)=
,则sinβ=( )
| 7 |
| 25 |
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
ξ~N(1,0.04)P(ξ>1)=( )
| A、0.2 | B、0.3 |
| C、0.4 | D、0.5 |