题目内容
一名篮球运动员投篮命中率为60%,在一次决赛中投10个球,则投中的球数不少于9个的概率为 .
考点:n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:分别求得投中9个篮球的概率、投中10个篮球的概率,再相加,即得所求.
解答:
解:投中9个篮球的概率为
×0.69×0.4,投中10个篮球的概率为0.610,
故投中的球数不少于9个的概率为
×0.69×0.4+0.610=4.6×0.69,
故答案为:4.6×0.69.
| C | 9 10 |
故投中的球数不少于9个的概率为
| C | 9 10 |
故答案为:4.6×0.69.
点评:本题主要考查相互独立事件的概率乘法公式的应用,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
阅读程序框图,若输出的函数值在区间[0,4]上,则输入的实数x的取值范围是( )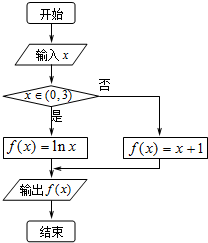

| A、{x∈R|-1≤x≤0或1≤x≤3} |
| B、{x∈R|-1≤x≤0或1≤x<3} |
| C、{x∈R|-1≤x≤0或1≤x≤e4} |
| D、{x∈R|-1≤x≤3} |