题目内容
8.设函数f(x)=x,(x≥1)函数g(x)=$\frac{1}{{x}^{2}-2x+4}$,(0<x$≤\sqrt{a}$+1,其中a>0).令h(x)为函数f(x)与g(x)的积函数.
(1)求函数h(x)的表达式,并求出其定义域;
(2)当h(x)的值域为[$\frac{1}{3}$,$\frac{1}{2}$]时,求实数a的取值范围.
分析 (1)直接相乘,可得函数h(x)的表达式,并求出其定义域;
(2)当h(x)的值域为[$\frac{1}{3}$,$\frac{1}{2}$]时,4≤x+$\frac{4}{x}$≤5,x+$\frac{4}{x}$=5时,x=1或4.可得2≤$\sqrt{a}$+1≤4,即可求实数a的取值范围.
解答 解:(1)h(x)=f(x)g(x)=$\frac{x}{{x}^{2}-2x+4}$(1≤x$≤\sqrt{a}$+1,其中a>0).
(2)h(x)=$\frac{1}{x+\frac{4}{x}-2}$,
∵h(x)的值域为[$\frac{1}{3}$,$\frac{1}{2}$],
∴4≤x+$\frac{4}{x}$≤5,
x+$\frac{4}{x}$=5时,x=1或4.
∴2≤$\sqrt{a}$+1≤4,
∴1≤a≤9.
点评 本题考查函数解析式的确定,考查函数的值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知sin2θ=$\frac{3}{5}$,且0<2θ<$\frac{π}{2}$,则$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$的值为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
16.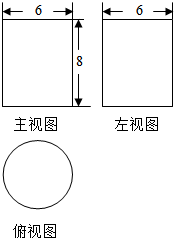 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |