题目内容
解关于x的不等式x2+x-m(m-1)>0(m∈R)
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:关于x的不等式x2+x-m(m-1)>0(m∈R),因式分解为(x-m)[x-(1-m)]>0.通过对m与1-m的大小分类讨论,再利用一元二次不等式的解法即可得出.
解答:
解:∵关于x的不等式x2+x-m(m-1)>0(m∈R),
∴(x-m)[x-(1-m)]>0.(*)
当m=1-m时,即m=
时,化为(x-
)2>0,∴x≠
.此时不等式的解集为{x|x≠
};
当m>1-m时,即m>
时,此时不等式的解集为{x|x>m或x<1-m};
当m<1-m时,即m<
时,此时不等式的解集为{x|x>1-m或x<m}.
综上可得:当m=
时,不等式的解集为{x|x≠
};
当m>
时,不等式的解集为{x|x>m或x<1-m};
当m<
时,不等式的解集为{x|x>1-m或x<m}.
∴(x-m)[x-(1-m)]>0.(*)
当m=1-m时,即m=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当m>1-m时,即m>
| 1 |
| 2 |
当m<1-m时,即m<
| 1 |
| 2 |
综上可得:当m=
| 1 |
| 2 |
| 1 |
| 2 |
当m>
| 1 |
| 2 |
当m<
| 1 |
| 2 |
点评:本题考查了一元二次不等式的解法、分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
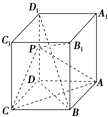 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证:
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.求证: 如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,M、N分别是BC和A1B1的中点.