题目内容
13.下列命题中正确的是( )| A. | x=2是x2-4x+4=0的必要不充分条件 | |
| B. | 在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,则该三角形△ABC为等腰三角形 | |
| C. | 命题“若x2<4,则-2<x<2”的逆否命题为“若x2≥4,则x≥2或x≤-2” | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
分析 A根据定义判断即可;
B利用正弦定理和诱导公式判断;
C根据逆否命题的定义判断;
D根据或命题和且命题以及非命题的等价关系可判断.
解答 解:A中x=2能推出x2-4x+4=0,但反之不一定,故应是充分不必要条件,故错误;
B中在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,由正弦定理可得sinAcosA=sinBcosB,
∴sin2A=sin2B,故A=B或A+B=$\frac{π}{2}$,则该三角形△ABC为等腰三角形或直角三角形,故错误;
C中命题“若x2<4,则-2<x<2”的逆否命题为“若x≥2或x≤-2,则x2≥4,”故错误;
D根据或命题和且命题以及非命题的等价关系可判断是正确的.
点评 考查了四中命题的逻辑关系和三角函数中正弦定理和诱导公式的应用.属于基础题型,应熟练掌握.

练习册系列答案
相关题目
3.(题类A)双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),过焦点F1的弦AB长为m(A,B在同一支上),另一个焦点为F2,则△ABF2的周长为( )
| A. | 4a-2m | B. | 4a | C. | 4a+m | D. | 4a+2m |
1.四面体ABCD的四个顶点都在球O的球面上,AB=2,BC=CD=1,∠BCD=60°,AB⊥平面BCD,则球O的表面积为( )
| A. | 8π | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{{8\sqrt{3}}}{3}π$ | D. | $\frac{16}{3}π$ |
18.方程lnx-x2+4x-4=0的实数根个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
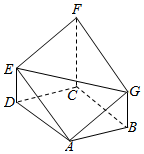 在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.
在如图所示的多面体ABCDEFG中,面ABCD是边长为2的菱形,∠BAD=120°,DE∥CF∥BG,CF⊥面ABCD,AG∥EF,且CF=2 BG=4.