题目内容
1.四面体ABCD的四个顶点都在球O的球面上,AB=2,BC=CD=1,∠BCD=60°,AB⊥平面BCD,则球O的表面积为( )| A. | 8π | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{{8\sqrt{3}}}{3}π$ | D. | $\frac{16}{3}π$ |
分析 由题意画出图形,设出底面三角形的外心G,找出四面体ABCD的外接球的球心O,通过求解直角三角形得到三棱锥的高,则答案可求.
解答 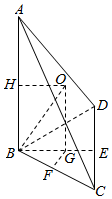 解:如图,∵BC=CD=1,∠BCD=60°
解:如图,∵BC=CD=1,∠BCD=60°
∴底面△BCD为等边三角形
取CD中点为E,连接BE,
∴△BCD的外心G在BE上,设为G,取BC中点F,连接GF,
在Rt△BCE中,由CE=$\frac{1}{2}$,∠CBE=30°,得BF=$\frac{1}{2}BC$=$\frac{1}{2}$,
又在Rt△BFG中,得BG=$\frac{\frac{1}{2}}{cos30°}=\frac{\sqrt{3}}{3}$,
过G作AB的平行线与AB的中垂线HO交于O,
则O为四面体ABCD的外接球的球心,即R=OB,
∵AB⊥平面BCD,∴OG⊥BG,
在Rt△BGO中,求得OB=$\sqrt{O{G}^{2}+B{G}^{2}}=\sqrt{{1}^{2}+(\frac{\sqrt{3}}{3})^{2}}=\frac{2\sqrt{3}}{3}$,
∴球O的表面积为$4π•(\frac{2\sqrt{3}}{3})^{2}=\frac{16π}{3}$.
故选:D.
点评 本题考查球的表面积的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
12.已知$z=\frac{2-i}{1+i}-{i^{2016}}$(i是虚数单位),则|z|=( )
| A. | 2 | B. | 4 | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{5}{2}$ |
6.对?α∈R,n∈[0,2],向量$\overrightarrow{c}$=(2n+3cosα,n-3sinα)的长度不超过6的概率为( )
| A. | $\frac{\sqrt{5}}{10}$ | B. | $\frac{2\sqrt{5}}{10}$ | C. | $\frac{3\sqrt{5}}{10}$ | D. | $\frac{2\sqrt{5}}{5}$ |
13.下列命题中正确的是( )
| A. | x=2是x2-4x+4=0的必要不充分条件 | |
| B. | 在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,则该三角形△ABC为等腰三角形 | |
| C. | 命题“若x2<4,则-2<x<2”的逆否命题为“若x2≥4,则x≥2或x≤-2” | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
10.已知函数f(x)=sin(ωx+φ)(ω>0)图象的两条相邻的对称轴的距离为$\frac{π}{3}$.若角φ的终边经过点P(1,-2),则f($\frac{7π}{3}$)等于( )
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
11.双曲线C:$\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1的左右焦点分别为F1,F2,双曲线C上一点P到右焦点F2的距离是实轴两端点到右焦点距离的等差数列,O为坐标原点,则点O到直线PF2的距离为( )
| A. | $\frac{6\sqrt{14}}{5}$ | B. | $\frac{12\sqrt{14}}{5}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{7}$ |