题目内容
2.已知向量$\overrightarrow a=(1,0)$,$\overrightarrow b=(1,2)$,则向量$\overrightarrow b$在向量$\overrightarrow a$方向上的投影为( )| A. | 1 | B. | 2 | C. | (1,0) | D. | (0,2) |
分析 求出$\overrightarrow{a}•\overrightarrow{b}$,代入向量的投影公式计算.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=1,$|\overrightarrow{a}|$=1,|$\overrightarrow{b}$|=$\sqrt{5}$,
∴向量$\overrightarrow b$在向量$\overrightarrow a$方向上的投影$\frac{a•\overrightarrow{b}}{|\overrightarrow{a}|}$=1.
故选:A.
点评 本题考查了平面向量的投影公式,属于基础题.

练习册系列答案
相关题目
12.已知$z=\frac{2-i}{1+i}-{i^{2016}}$(i是虚数单位),则|z|=( )
| A. | 2 | B. | 4 | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{5}{2}$ |
13.下列命题中正确的是( )
| A. | x=2是x2-4x+4=0的必要不充分条件 | |
| B. | 在△ABC中,三边a,b,c所对的角分别为A,B,C,若acosA=bcosB,则该三角形△ABC为等腰三角形 | |
| C. | 命题“若x2<4,则-2<x<2”的逆否命题为“若x2≥4,则x≥2或x≤-2” | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
10.已知函数f(x)=sin(ωx+φ)(ω>0)图象的两条相邻的对称轴的距离为$\frac{π}{3}$.若角φ的终边经过点P(1,-2),则f($\frac{7π}{3}$)等于( )
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
17.执行如图所示程序图,若N=7时,则输出的结果S的值为( )
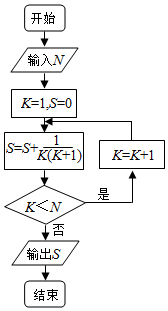

| A. | $\frac{8}{7}$ | B. | $\frac{6}{5}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{6}$ |
11.双曲线C:$\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1的左右焦点分别为F1,F2,双曲线C上一点P到右焦点F2的距离是实轴两端点到右焦点距离的等差数列,O为坐标原点,则点O到直线PF2的距离为( )
| A. | $\frac{6\sqrt{14}}{5}$ | B. | $\frac{12\sqrt{14}}{5}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{7}$ |