题目内容
15.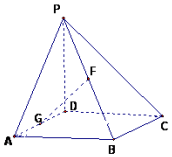 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.(Ⅰ)求证:CD⊥PA;
(Ⅱ)证明:GF⊥平面PBC.
分析 (I)以D为原点建立空间直角坐标系,利用$\overrightarrow{PA}$•$\overrightarrow{DC}$=0,证得PA⊥CD;
(Ⅱ)利用$\overrightarrow{FG}$•$\overrightarrow{CB}$=0,$\overrightarrow{FG}$•$\overrightarrow{PC}$=0,去证GF⊥平面PCB.
解答 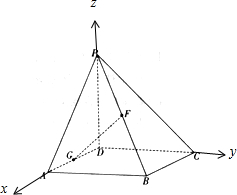 证明:(I)以D为原点建立空间直角坐标系则A(2,0,0)B(2,2,0)C(0,2,0)P(0,0,2)F(1,1,1)
证明:(I)以D为原点建立空间直角坐标系则A(2,0,0)B(2,2,0)C(0,2,0)P(0,0,2)F(1,1,1)
$\overrightarrow{PA}$=(2,0,-2),$\overrightarrow{DC}$=(0,2,0),
∴$\overrightarrow{PA}$•$\overrightarrow{DC}$=0,∴$\overrightarrow{PA}$⊥$\overrightarrow{DC}$,
∴PA⊥CD;
(Ⅱ)设G(1,0,0)则$\overrightarrow{FG}$=(0,-1,-1),$\overrightarrow{CB}$=(2,0,0),$\overrightarrow{PC}$=(0,2,-2)
∴$\overrightarrow{FG}$•$\overrightarrow{CB}$=0,$\overrightarrow{FG}$•$\overrightarrow{PC}$=0,
∴FG⊥CB,FG⊥PC,
∵CB∩PC=C,
∴GF⊥平面PCB.
点评 本题考查线面、面面位置关系的证明.借助于空间向量的运算,降低了思维难度,增加了解题方法.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
5.点P为正四面体ABCD的棱BC上任意一点,则直线AP与直线DC所成角的范围是( )
| A. | $[\frac{π}{6},\frac{π}{2}]$ | B. | $[\frac{π}{4},\frac{π}{3}]$ | C. | $[\frac{π}{3},\frac{π}{2}]$ | D. | $[\frac{π}{6},\frac{π}{4}]$ |
3.已知函数f(x)(x∈R,且x≠1)的图象关于点(1,0)对称,当x>1时f(x)=loga(x-1),且f(3)=-1,则不等式f(x)>1的解集是( )
| A. | $(-3,\frac{3}{2})$ | B. | $(-∞,-3)∪(\frac{3}{2},+∞)$ | C. | $(-∞,-1)∪(\frac{3}{2},+∞)$ | D. | $(-∞,-1)∪(1,\frac{3}{2})$ |
20.下列函数中,在区间($\frac{π}{2}$,π)上为增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=tanx | D. | y=-tanx |
5.已知($\sqrt{3}$+i)•z=-i(i是虚数单位),那么复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
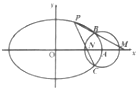 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的长轴长为4,焦距为$2\sqrt{3}$,以A为圆心的圆(x-2)2+y2=r2(r>0)与椭圆相交于B、C两点.