题目内容
7. 如图,△ABC中,∠BAC=60°,BE、CF分别是∠ABC和∠ACB的角平分线,且BE、CF交于D点,求证:DE=DF.
如图,△ABC中,∠BAC=60°,BE、CF分别是∠ABC和∠ACB的角平分线,且BE、CF交于D点,求证:DE=DF.
分析 作辅助线在CB上截取CG=CE,可证出△CED≌△CGD(SAS),即可得出∠EDC=∠GDC,ED=GD,根据三角形的内角和定理,得出∠EBC+∠FCB=60°,在△DBC中,即可求出∠FDE=∠BDC=120°,可证出△BFD≌△BGD,即可得出FD=ED
解答 证明:由三角形内角和定理,在△ABC中,
2∠EBC+2∠FCB+60°=180°,
解得∠EBC+∠FCB=60°,
在△DBC中,∠BDC=180°-(∠EBC+∠FCB)=180°-60°=120°,
∴∠FDE=∠BDC=120°,
在CB上截取CG=CE,由∠ECD=∠GCD,DC=DC,
得:△CED≌△CGD(SAS),
∴∠EDC=∠GDC,ED=GD,
由(1)知∠BDG+∠GDC=120°,
又∵∠BDG+2∠GDC=180°,
解得:∠BDG=∠GDC=∠EDC=60°
在△BFD和△BGD中,∠FBD=∠GBD,∠FDB=∠GDB=60°,BD=BD,
∴△BFD≌△BGD,
∴FD=DG,
∴FD=ED.
点评 此题综合考查角平分线的定义、三角形的内角和定理和全等三角形的判定和性质等知识点,难度适中,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知直线2x+y-10=0过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的焦点且与该双曲线的一条渐近线垂直,则该双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ |
12.设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,则a0+a2+…+a2n的值是( )
| A. | $\frac{1}{2}$(3n-1) | B. | $\frac{1}{2}$(3n+1) | C. | 3n | D. | 3n+1 |
16.△ABC的内切圆与三边AB,BC,CA的切点分别为D,E,F,已知B(-$\sqrt{2}$,0),C($\sqrt{2}$,0).内切圆圆心I(1,t),t≠0,设点A的轨迹为R,求R的方程.
17.已知全集U=R,集合A={x|x2≥4},集合B={x|x>1},则∁U(A∪B)=( )
| A. | {x|-2<x<2} | B. | {x|1≤x≤2} | C. | {x|-2<x≤1} | D. | {x|-2≤x<1} |
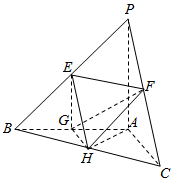 如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.
如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2. 如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.