题目内容
在平面直角坐标系xOy中，以Ox为始边，角α的终边与单位圆O的交点B在第一象限，已知A(－1,3)．
(1)若OA⊥OB，求tan α的值．
(2)若B点横坐标为
，求S△AOB.
解析：(1)由题可知：A(－1,3)，B(cos α，sin α)，
＝(－1,3)，
＝(cos α，s
in α)，
OA⊥OB，得·＝0，
所以－cos α＋3sin α＝0，tan α＝
.
(2)由(1)|OA|＝
＝
， 记∠AOx＝β，β∈
，
所以sin β＝
＝
，cos β＝
＝－
，
∵|OB|＝1，cos α＝，得sin α＝
＝
，
sin∠AOB＝sin(β－α)＝×＋×＝，
所以S△AOB＝
|AO||BO|sin∠AOB＝××1×＝
.
练习册系列答案
相关题目
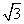cos x(0≤x<2π)取得最大值时，x＝________.
＝________.
，则角α的最小正值为__________．
，∠CAB＝
，则∠AOB对应的劣弧长为__________．
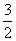，则线段CD的长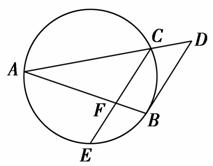为________．
(t为参数)的倾斜角为________．